Force and Motion(বল ও গতি )

Rest and Motion(স্থিতি ও গতি )

যদি কোনো বস্তু তার পারিপার্শ্বিকের সাপেক্ষে স্থির থাকে তাকে স্থির বস্তূ বলে । অপরপক্ষে যদি একটি বস্তু পারিপার্শ্বিকের সাপেক্ষে তার অবস্থানের পরিবর্তন হয় তাহলে বস্তুটিকে গতিশীল বস্তু বলে ।স্থিতি ও গতির ধারণাটি হল আপেক্ষিক । চরম স্থিতিশীল বা চরম গতিশীল বলে কোনো বা বস্তু হয় না ।এই পৃথিবীতে  আমরা গতি পরিমাপ করি  মাটি বা ভূমির সাপেক্ষে । ভূমি বা পৃথিবীকে স্থির বস্তু হিসাবে ধরা হয় । কিন্তু প্রকৃত পক্ষে পৃথিবী সূর্যের চর্তুর্দিকে ঘুরছে । সূর্যের সাপেক্ষে পৃথিবীর সব বস্তুই গতিশীল ।আবার সূর্যেও কোনো পরম স্থির বস্তু নয় ।সূর্যেও মহাকাশে গতিশীল অবস্থায় আছে । সুতরাং স্থিতি ও গতির ধারণাটি একটি আপেক্ষিক ধারণা ।প্লাটফর্মে দাঁড়িয়ে থাকা ব্যক্তি লক্ষ্য করে ট্রেন গতিশীল । কিন্তু ট্রেনের ভিতরের যাত্রী লক্ষ্য করে প্লাটফর্ম গতিশীল । কোনো বস্তু কোনো দর্শকের সাপেক্ষে স্থির মনে হতে পারে , ওই একই বস্তু অপর কোনো দর্শকের কাছে গতিশীল মনে হতে পারে ।গতিতে (If an object remains static with respect to its surroundings it is said to be in rest.On the other hand if an object changes its position with respect to its surrounding it is said to be in motion.The concept of rest and motion is relative.There is no absolute rest or absolute motion.In earth we measure motion with rest to the ground.The ground( earth)  is taken as rest.But in actual case the earth is in motion around the sun.When reference point is taken in  sun then every object on earth is in motion.Sun is also not in absolute rest.So the concept of rest and motion is a relative one.A man standing on platform sees the  train moving.A man inside the train sees a person standing on platform moving in opposite direction.An object may seem to be at rest to an observer and the same object may seem to be in motion with respect to another observer.So it depends on reference point).

     

গতির প্রকার ভেদ -চলন ও ঘূর্ণন (Types of motion - translation and rotation )
চলন গতি( Translational motion) -এই গতিতে বস্তুকণা সরলরেখায় গতিশীল হয় ।এই ধরনের গতিতে বাস্তুকনার অবস্থানের পরিবর্তন হয়, কিন্তু অভিমুখের কোনো পরিবর্তন হয় না । ( In this motion particle moves in a straight line.Here an object changes its position but not its direction.)

     

ঘূর্ণন গতি (Rotational motion) - যদি একটি কণিকা  বৃত্তাকার পথে গতিশীল থাকে সেই গতিকে ঘূর্ণন গতি বলে ।(If a particle moves in a circle then its motion is rotational one.)

         

জটিল গতি (Mixed or complex motion )-যদি কোনো বস্তুর মধ্যে চলন ও ঘূর্ণন উভয় প্রকার গতি থাকে সেই গতিকে জটিল গতি বলে ।(It is a combination of  translational and rotational motion.Example - motion of a rotational top).

         

অন্য প্রকারের গতি (Other type of motions)
পর্যাবৃত্ত গতি (Periodic motion) - যে ধরনের গতি একটি নিৰ্দিষ্ট সময় অন্তর পুনরাবৃত্ত হয় তাকে পর্যাবৃত্ত গতি বলে ।যেমন - পৃথিবীর নিজ অক্ষের উপর ঘূর্ণন গতি , সূর্যের চতুর্দিকে পৃথিবীর গতি ।(A motion that repeats itself after a certain interval of time is called as Periodic motion.Example- Spinning motion of earth around its axis, motion of earth around sun etc.)

          

সরল দোলো গতি (Simple Harmonic Motion) - একটি বস্তু নিৰ্দিষ্ট সময়ের ব্যবধানে যদি একটি নিৰ্দিষ্ট বিন্দু সাপেক্ষে বারবার একই পথে যাতায়াত করে তবে তার গতিকে সরল দোলো গতি বলে ।যেমন - সরল দোলকের বস্তু পিন্ডের গতি ।(A periodic motion in a straight line and the force acting on the particle is always directed towards a  certain point on the straight line is known as SHM.Example- Motion of  the bob of a simple pendulum.)

       

Explanation of certain terms.
সরন(Displacement)  -

কোন গতিশীল বস্তুর সময়ের সঙ্গে একটি নিৰ্দিষ্ট দিকে স্থান বা অবস্থানের পরিবর্তনকে সরণ বলে ।বস্তুটির প্রথম ও শেষ অবস্থান সরলরেখা দ্বারা যোগ করলে যে দূরত্ব পাওয়া যায় সেটি  বস্তুটির সরণের পরিমাপ ।বস্তুটির প্রাথমিক অবস্থান থেকে শেষ অবস্থানের  অভিমুখ  বস্তুটির সরণের অভিমুখ নিৰ্দেশ করে ।যদি একটি বস্তুকণা প্রথমে পূর্বদিকে 4 m এবং পরে উত্তরদিকে 3 m  গমন করে সরণ হবে 5 m. , 7(4+3) মিটার  নয় ।কারণ - √( 3² + 4²) = 5  |সরণ ভেক্টর রাশি ।(It is the shortest distance   in certain direction in straight  line between the initial and final position of a moving object.It is a vector quantity.) Example - If an object moves 4 m in eastward  and then 3 m in northward direction. Then its displacement is 5 m ( square root of ( 3² + 4²) It is not 7 m (3+4).)

দূরত্ব (Distance):

কোনো গতিশীল বস্তুকণা তার যাত্রাকালে মোট যে পথ অতিক্রম করে তাকে দূরত্ব বলে ।দূরত্বের মান আছে কিন্তু অভিমুখ নেই তাই এটি স্কেলার রাশি ।নীচের উদাহরণে বস্তুকণা P থেকে Q তে এবং Q থেকে R বিন্দুতে গমন করে ।এক্ষেত্রে অতিক্রান্ত দূরত্ব হয় 7 মিটার(4+3) । 

     

দূরত্ব ও সরণের মধ্যে পার্থক্য   

দূরত্ব	সরণ
1.কোনো বস্তুকণার প্রাথমিক ও শেষ অবস্থানের মোট অতিক্রান্ত পথের দৈর্ঘ্যকে দূরত্ব বলে ।	1.কোনো বস্তুকণার প্রাথমিক ও শেষ অবস্থানের সরলরেখিক সরণ বলে ।
2.দূরত্বের নিৰ্দিষ্ট মান আছে  কিন্তু কোনো অভিমুখ নেই তাই এটি স্কেলার রাশি ।	2.সরণের মান ও অভিমুখ দুই আছে তাই সরণ ভেক্টর রাশি ।
3.গতিশীল কণার দূরত্ব কখনো শূন্য হয় না ।	3.গতিশীল কণার সরণ শূন্য হতে পারে ।

দ্রুতি (Speed) - সরল বা বক্রপথে কোনো বস্তুকণা একক সময়ে যে দূরত্ব অতিক্রম করে তাকে ওই বস্তু কণার দ্রুতি বলে । অর্থাৎ চলমান বস্তুকণার দূরত্ব অতিক্রম করার হারকে দ্রুতি বলে ।এটি একটি স্কেলার রাশি ।SI পদ্ধতিতে দ্রুতির একক m/s এবং CGS  পদ্ধতিতে একক cm/s |(It is a rate at which a moving object traverses distance.Speed = Distance traversed / Time taken.It is a scalar quantity.It's unit is m/s in SI and cm/s in CGS System.)

দ্রুতির মাত্রা - দূরত্বের মাত্রা / সময়ের মাত্রা =[L/T] = [LT⁻¹]

বিভিন্ন প্রকার দ্রুতি -

1. সম দ্রুতি(Un iform Speed): সরল বা বক্রপথে কোনো গতিশীল বস্তুকণা সর্বদা সমান সময়ের ব্যবধানে সমান দূরত্ব অতিক্রম করলে তবে বাস্তুকনার দ্রুতিকে সমদ্রুতি বলে ।

2.অসম দ্রুতি ( Non-uniform Speed) :

সরল বা বক্রপথে কোনো চলমান বস্তুকণা সমান সময়ের ব্যবধানে সমান দূরত্ব অতিক্রম  না করলে বস্তু কনার দ্রুতিকে অসমদ্রুতি বলে ।

3. গড় দ্রুতি (Average Speed) :

অসম দ্রুতি যুক্ত বস্তুকণার মোট অতিক্রান্ত দূরত্ব কে মোট্ সময় দিয়ে ভাগ করলে যে দ্রুতি হয়  তাকে গড় দ্রুতি বলে । মনেকরি একটি বস্তুকণা ₁t সময়ে S₁ দূরত্ব , t₂ সময়ে S₂,এবং t₃ সময়ে S₃ দূরত্ব অতিক্রম করে ।

 ∴ গড় দ্রুতি  = মোট অতিক্রান্ত দূরত্ব / মোট সময়  = (S₁ +S₂ +S₃)/(t₁+t₂ +t₃) 

তাৎক্ষণিক দ্রুতি (Instantaneous Speed): কোনো বস্তুকণার দ্রুতি যদি অসম হয়  তাহলে ওর গতিপথের কোনো যে কোনো বিন্দুতে যে দ্রুতি হয় তাকে তাৎক্ষণিক দ্রুতি বলে ।

বেগ (Velocity )- একক সময়ে কোনো গতিশীল বস্তুকণা নিৰ্দিষ্ট দিকে যে দূরত্ব অতিক্রম করে তাকে বেগ বলে ।অর্থাৎ চলমান বস্তুকণার সময়ের সাপেক্ষে সরণের পরিবর্তনের হারকে বেগ বলে ।বেগ একটি ভেক্টর রাশি ।এর একক দ্রুতি র  এককের সমান ।(It is a rate of   change of displacement of a moving object.It is a vector quantity since displacement is vector quantity.Its units are same as units of speed.)

বিভিন্ন প্রকারের বেগ (Types of Velocity):

সম বেগ (Uniform Velocity) : সময়ের সঙ্গে কোনো বস্তুর বেগের মান ও অভিমুখ অপরিবর্তিত থাকলে বস্তুটির বেগকে সম বেগ বলে ।

অসম বেগ (Non -uniformVelocity):  সময়ের সঙ্গে কোনো বস্তুর বেগের মান  বা অভিমুখ  অথবা দুটোই পরিবর্তণ হলে বস্তুটির বেগকে অসম বেগ বলে ।

গড়বেগ (Average Velocity): বস্তু অসম বেগে  গতিশীল হলে বিভিন্ন বেগে অতিক্রান্ত মোট সরণকে মোট সময় দিয়ে ভাগ করলে যে বেগ হয় তাকে গড়বেগ বলে ।

গড়বেগ = মোট সরণ /মোট সময়  ।

                                                       দ্রুতি ও বেগের মধ্যে পাৰ্থক্য 

দ্রুতি	বেগ
i) একক সময়ে গতিশীল বস্তুকণা যে দূরত্ব অতিক্রম করে তাকে দ্রুতি  বলে ।	i) গতিশীল বস্তুকণা নিৰ্দিষ্ট দিকে একক সময়ে  যে দূরত্ব অতিক্রম করে তাকে  বেগ বলে ।
ii) দ্রুতির মান আছে ,অভিমুখ নেই ,তাই স্কেলার রাশি ।	ii) বেগের মান ও অভিমুখ দুইই আছে তাই ভেক্টর রাশি ।
iii) দ্রুতি কখনো ঋনাত্বক হয় না , কারণ দূরত্ব সর্বদা ধনাত্বক হয় ।	iii) বেগ ঋনাত্বক হতে পারে , কারণ এর অভিমুখ আছে ।
iv) সমদ্রুতি সম্পন্ন বস্তু সমবেগ সম্পন্ন নাও হতে পারে ।	iv) সমবেগ সম্পন্ন বস্তু সর্বদা সম দ্রুতি সম্পন্ন হবেই ।
v) গড় দ্রুতি কখনও শুন্য হবে না ।	v) গড় বেগ শুন্য হতে পারে ।

ত্বরণ (Acceleration )- কোনো বস্তুকণা ক্রমবর্ধমান বেগ নিয়ে চললে সময়ের সঙ্গে কণাটির বেগ বৃদ্ধির হারকে  ত্বরণ বলে ।অর্থাৎ একক সময়ে বেগের যে বৃদ্ধি হয় তাকে ত্বরণ বলে । 

ত্বরণ  = বেগের বৃদ্ধি /সময়  =  (v -u)/t [ u = প্রাথমিক বেগ ,v = অন্তিম বেগ , t = অতিক্রান্ত সময় ।]

ত্বরণের মান  ও দিক উভয়েই থাকায় ইহা একটি ভেক্টর রাশি ।

ত্বরণের একক : CGS পদ্ধতিতে ত্বরণের একক  cm/s² 

       SI পদ্ধতিতে এর একক  m/s²

ত্বরণের মাত্রা  : ত্বরণের মাত্রা = বেগের মাত্রা /সময়ের মাত্রা  = [LT⁻¹/T] = [LT⁻²]

 

বিভিন্ন প্রকার তব্রন( Different types of acceleration):

i) সম ত্বরণ (Uniform Acceleration): কোনো বস্তুকণার বেগ সমান সময়ের ব্যবধানে সমপরিমানে বৃদ্ধি পেলে বস্তুটির ত্বরণ কে সম ত্বরণ ।উদাহরণ - কোনো স্থানে বস্তু অভিকর্ষের অধীনে সম ত্বরণে নিচে পড়ে ।

ii) অসম ত্বরণ (Non- uniform acceleration) -কোনো বস্তুকণার বেগ সমান সময়ের ব্যবধানে সমপরিমানে বৃদ্ধি না পেলে বস্তুটির ত্বরণকে অসমত্বরণ বলে ।যেমন - সরল দোলকের বস্তুপিণ্ডের ত্বরণ বিভিন্ন স্থানে বিভিন্ন হয় । দুই প্রান্তিক অবস্থানে ত্বরণ সর্বোচ্চ হয় ।

কোনো বস্তুর বেগ ও ত্বরণ পরস্পর বিপরীতও হতে পারে ।উদাহরণ - কোনোবস্তুকে উপরের দিকে ছোড়া হলে বেগ উপরের দিকে ক্রিয়া করে কিন্তু অভিকর্ষজ ত্বরণ নিচের কাজ করে ।

মন্দন (Reterdation): কোনো বস্তুকণা ক্রমহ্রাসমান বেগ নিয়ে চললে বস্তুটির বেগ হ্রাসের হারকে মন্দন বলে ।মন্দনকে ঋনাত্বক ত্বরণ বলে ।

 ত্বরণ না থাকলেও বেগ থাকতে পারে - বস্তু সমবেগে চললে ত্বরণ থাকে না কিন্তু বেগ থাকে ।সরল দোলকের বস্তুপিন্ড যখন মধ্য অবস্থানে থাকে তখন ত্বরণ শূন্য কিন্তু বেগ সর্বচ্চো ।

বস্তুর বেগ না থাকলেও ত্বরণ থাকতে পারে - কোনো বস্তুকে উপরের দিকে ছোড়া হলে বস্তুটির সর্বোচ্চ অবস্থানে বেগ হলেও উহার উপর অভিকর্ষজ ত্বরণ কাজ করে ।

বেগ সময় লেখচিত্র (Velocity timegraph):

 

উপরের চিত্রে সমবেগে গতিশীল কণার গতিবেগ -সময় লেখচিত্র দেখানো হয়েছে । এক্ষেত্রে বস্তুর ত্বরণ শুন্য হয় ।

উপরের লেখ চিত্র সমত্বরণে গতিশীল বস্তুকণার গতিবেগ -সময় লেখচিত্র প্রদর্শন করে ।

 

গতির সমীকরণগুলির গাণিতিক প্রকাশ (Mathematical Representation of the equations of motion in algebraic forms)
 মনে করি একটি বস্তু কণা  v সমবেগে চলছে ।অতএব 1 সেকেন্ডে বস্তু কোনটি পথ অতিক্রম করে  v  একক । t সেকেন্ডে কণাটি S দূরত্ব অতিক্রম করলে  S  = vt হবে । 

অতএব গতীয়  সমীকরণটি হল -

1) S = vt 

(Let a particle moves with uniform velocity v After time t it traverses a distance s then equation is:
1)s = vt.)

লেখ চিত্রের সাহায্যে  S = vt সমীকরণের প্রতিষ্ঠা :

এক্ষেত্রে বস্তুটি যেহেতু সমবেগে চলছে বেগ - সময় লেখচিত্রটি সময় অক্ষের সমান্তরাল হয় ।

OA = CD বস্তুটির সমবেগে  v নিৰ্দেশ করে ।অতিবাহিত সময় t =t₂ - t₁ = DE 

t সময়ে অতিক্রান্ত দূরত্ব = DEBC আয়তক্ষেত্রের ক্ষেত্রফল  = CD x DE =v t |

2) v = u + at সমীকরণের প্রকাশ :

মনেকরি কোনো গতিশীল বস্তুর প্রাথমিক বেগ = u ,t সময় পরে বস্তুটির অন্তিম বেগ = v এবং ত্বরণ = a 

t সময়ে বেগের পরিবর্তন  v - u |

∴ বস্তুটির ত্বরণ (a) = বেগের পরিবর্তন /সময়  =( v -u )/t 

বা  v - u = at 

    ∴ v = u + at 

(If a particle starts with initial velocity u  after time t it achieves a velocity v then its acceleration a = (v- u)/t and the equation is  2) v =  u + at) 

বেগ - সময় লেখচিত্র থেকে  v = u + at সম্পর্কটি প্রতিষ্ঠা :

যাত্রা মুহূর্ত থেকে বস্তুটির ত্বরণ a , প্রাথমিক বেগ = u (OA) ,t (OD)সময় পরে বেগ v ( DB = DC + CB)

ত্বরণ a = (DB -OA )/OD = (DB - CD)/OD ( OA = CD )

= (v - u)/t

⇒ at = v - u

∴ v = u + at    

    3. S=ut + 1/2 a t²² সমীকরণের  প্রতিষ্ঠা :

বস্তুটির প্রাথমিক বেগ  = u ত্বরণ = a ,t সময় পরে বেগ = v .

বস্তুটির গড় বেগ = ( u + v)/2 

t সময় ধরে বেগ এই গড় বেগ অপরিবর্তিত থাকে ।

∴  S =( u +v)/2 x t 

⇒ S =  ( u + u + at)/2 x t ( ∵ v = u + at)

⇒ S = ut + 1/2 a t² 

(The particle traverses a distance s then average velocity va = (u+v)/2 and distance s = va* t =(u+v) *t/2 =(u + u+at)*t/2 = ut + 1/2 at²
Hence 3 ) s = ut + 1/2 at²)

লেখচিত্রের সাহায্যে S = ut + 1/2 a t²  সমীকরণটির প্রতিষ্ঠা :

এক্ষেত্রে প্রাথমিক বেগ u এবং ত্বরণ  a হলে t সময়ে অতিক্রান্ত দূরত্ব S উপরের চিত্রে ODBA ট্রাপিজিয়ামের ক্ষেত্রফলের সমান হৰে ।এখন ODBA ট্রাপিজিয়ামের ক্ষেত্রফল = ODCA আয়াতক্ষেত্রের ক্ষেত্রফল  + ABC ত্রিভুজের ক্ষেত্রফল          

= OD x CD + 1/2 AC x BC

= ut + 1/2 x t x (BD- CD) 

= ut +1/2t at

= ut + 1/2 at²

∴  S = ut + 1/2 at²

           4) v³ = u² + 2 a S সমীকরণটির  প্রতিষ্ঠা :

মনেকরি a সমত্বরণে গতিশীল বস্তুকণার প্রাথমিক বেগ u , t সময় পরে বেগ v এবং অতিক্রান্ত দূরত্ব S হলে , v = u +at এবং   S = ut + 1/2 at² হয় ।

v = u +at সমীকরণটি বর্গ করে পাই ,

    v² = ( u + at)²

    ⇒ v²  = u² +2 uat + a² t² 

              = u²  + 2a(ut + 1/2 at² )

              = u² + 2aS

∴ v² =  u² + 2a S 

লেখচিত্রের সাহায্যে v² =  u² + 2a S  সমীকরণটির প্রতিষ্ঠা :

⇒মনেকরি একটি বস্তুর প্রাথমিক বেগ u, a সমত্বরণ সহ t সময় চলার পর বেগ হয় v = u +at এবং অতিক্রান্ত দূরত্ব S |

                

এখন অতিক্রান্ত দূরত্ব S = OABD ট্রাপিজিয়ামের ক্ষেত্রফল 

⇒ S = 1/2( OA + BD) x OD

       = 1/2 (OA + BD) x OD x BC/BC

       = 1/2 ( OA +BD) x OD x(BD - CD)/BC

       = 1/2 (OA + BD)(BD - OA) х OD/BC

       = 1/2 (BD² - OA²) х OD/BC

       = 1/2 ( v² - u²) х t/(at) ( ∵ BC(at ) = BD(v) - CD(u))

        = 1/2 ( v² - u²) х1/a

  ⇒ 2aS = v² - u²

∴ v²  = u² + 2 a S 

নিউটনের প্রথম গতিসূত্র (Newton's First law of motion.)বাহিরের থেকে বল প্রয়োগ না করলে স্থির বস্তু চিরকাল স্থির থাকবে সচল বস্তু চিরকাল সমবেগে সরলরেখায় গতি বজায় রাখবে ।

এই গতিসূত্র থেকে বলের সংগা  ও পদার্থের জাড্য ধৰ্ম সম্পর্কে জানা যায় ।

বলের সংজ্ঞা : বাহিরের থেকে যা প্রয়োগ করলে বস্তুর স্থিতিশীল বা গতিশীল অবস্থার অথবা তার আকৃতির কিংবা গতির অভিমুখের পরিবর্তন হয় বা হওয়ার উপক্রম করে তাকে বল বলে ।

বলের প্রকারভেদ :

আমরা দৈনন্দিন জীবনে যে বলের সম্মুখীন হই তাদের সাধারণভাবে দুই ভাগে ভাগ করা যায় ।

i) প্রতিমিত বল  ii) অপ্রতিমিত বল 

i) প্রতিমিত বল - কোনো বস্তুর উপর একাধিক বলের ক্রিয়ায় যখন লব্ধি বল শূন্য হয় ওই বলগুলিকে একত্রে প্রতিমিত বল বলে । যেমন - মেঝের উপর অবস্থিত কোনো বস্তুকে ঠেলার চেষ্টা করলে বস্তুটি যদি গতিশীল না হয় তাহলে প্রযুক্ত বাহ্যিক বল ও ঘর্ষণ বল প্রতিমিত বল গঠন করে । প্রযুক্ত বল ও ঘর্ষণ বল পরস্পর সমান ও বিপরীত মুখী হয় ।

ii) অপ্রতিমিত বল : - কোনো বস্তুর উপর ক্রিয়াশীল একাধিক বলের লব্ধি শূন্য না হলে ওই বলগুলিকে একত্রে অপ্রতিমত  বল বলে । যেমন -একটি ভারী বাক্সকে মেঝের উপর টানলে এক্ষেত্রে প্রযুক্ত বল ঘর্ষণ বল অপেক্ষা বেশি হয় । এখানে প্রযুক্ত বল ও ঘর্ষণ বল একত্রে অপ্রতিমিত বল বলে ।

বস্তুর জাড্য ( Inertia of Matter):

পদার্থের যে ধর্মের জন্য স্থির বস্তু  বা গতিশীল বস্তু  যে অবস্থায় আছে সেই অবস্থা বজায় রাখার চেষ্টা করে সেই ধর্মকে পদার্থের জাড্য ধৰ্ম বলে ।

জাড্য দুই প্রকার - i) স্থিতি জাড্য ii) গতি জাড্য 

i)স্থিতি জাড্য - স্থিরবস্তুর চিরকাল স্থির থাকার প্রবণতাকে স্থিতি জাড্য বলে ।

উদাহরণ - 1.কোনো গাড়ি হঠাৎ চলতে শুরু করলে গাড়ির মধ্যে দাঁড়িয়ে থাকা কোনো যাত্রী পিছনের দিকে হেলে যায় ।গাড়ি যখন স্থির থাকে তখন যাত্রীর গোটা শরীর স্থির থাকে । কিন্তু গাড়ি চলতে শুরু করলে যাত্রীর শরীরের নিচের অংশ তৎক্ষণাৎ গতিশীল হয় , শরীরের উপরের অংশ স্থিতি জাড্যের জন্য স্থির থাকতে চায় ।তাই যাত্রী পিছনের দিকে হেলে পড়ে । 

ii)গতিজাড্য - গতিশীল বস্তুর সমবেগে সরলরেখায় চলার প্রবণতাকে গতিজাড্য বলে ।

উদাহরণ - 1. কোনো চলন্ত গাড়ি হঠাৎ থামলে যাত্রীরা সামনের দিকে ঝুঁকে পড়ে ।গতিজাড্যের জন্যে এইরকম হয় । গাড়ি থামলে শরীরের নীচের মান তৎক্ষণাৎ স্থির হয় ।কিন্তু শরীরের উপরের অংশ গতিজাড্যের জন্য গতি বজায় রাখার চেষ্টা করে । ফলস্বরূপ যাত্রী সামনের দিকে হেলে পড়ে । 
(Inertia of matter - A body maintains its state of rest or of motion unless it is acted upon by an external force.If a body is in rest position then it will remain  in that rest position always ie a rest body always maintains its position of rest ,this property of matter is known as Inertia of rest.If a body is in motion then it will also remain in that motion in straight line. This is also inertia . It is known as Kinetic inertia.)

বলের সংযোজনের সামান্তরিক সূত্র (Parallelogram law of addition of forces):

কোনো বস্তুর উপর দুটি বল ক্রিয়া করলে তাদের সম্মিলিত ক্রিয়ায় একটি লব্ধি বল পাওয়া যায় যার প্রভাবে বস্তুটি গতিশীল হয় ।এই লব্ধি বলের মান ও অভিমুখ বলের সামান্তরিক সূত্র থেকে জানা যায় ।

সূত্রটি হল - 

একই বিন্দুতে ক্রিয়া রত দুটি সমজাতীয় বলকে কোনো সামান্তরিকের দুটি সন্নিহিত বাহুদ্বারা মানে ও দিকে সূচিত করলে , সামান্তরিকের সন্নিহিত বাহুদুটির ছেদবিন্দু দিয়ে অঙ্কিত কর্ণ ওই বলদুটির লব্ধিকে মানে ও দিকে প্রকাশ করবে ।

       

উপরের চিত্রে A ও B  বলের লব্ধি হল R  ।

উদাহরণ - পাখির আকাশে ওড়া বলের সামান্তরিক সূত্রের সাহায্যে ব্যাখ্যা করা যায় ।

পাখি তার দুটি ডানা দিয়ে যথাক্রমে AO ও BO অভিমুখে বল প্রয়োগ করে । বায়ু প্রতিক্রিয়া বল যথাক্রমে OA ও OB অভিমুখে প্রয়োগ করে । এদের লব্ধি OC অভিমুখে কাজ করে । OC অভিমুখে পাখিটি গমন করে ।

বলের বিভাজন (Resolution of force):

বলের বিভাজন বলতে কোনো বলকে দুই বা ততোধিক নিৰ্দিষ্ট দিকে এমনভাবে বিভাজিত করা বোঝায় যাতে বিভাজিত বলগুলির লব্ধি প্রদত্ত বলটির সমান হয় ।

বলের বিভাজন হল বলের সংযোজনের বিপরীত প্রক্রিয়া । প্রদত্ত বলটিকে কোনো সামান্তরিকের কর্ণ হিসাবে ধরে  সামান্তরিকটির দুই সন্নিহিত বহু বলের দুই উপাংশ সূচিত করবে ।

         

উপরের চিত্রেকর্ণ OC বলের দুই বিভাজিত অংশ হল OA এবং OB |বিপরীত ক্রমে বলাযায় OA এবং OB বলের লব্ধি হল OC  ।

বলের লম্ব উপাংশে বিভাজন :

            

R বলের অনুভূমিক দিকে( OX) উপাংশ হল OQ = R Cos θ ,এবং উলম্ব দিকের(OY)উপাংশ  OP  = R Sin θ 
বলের বিভাজনের বাস্তবিক প্রয়োগ :

বলের বিভাজনকে কাজে লাগিয়ে রোলার ঠেলা ও টানা সহজে বোঝা যায় ।

রোলার ঠেলা - 

      

ঠেলার সময় OA অভিমুখে বল প্রয়োগ করা হয় । এর উলম্ব ও অনুভূমিক উপাংশ হলো  V ও H | V  অংশ নীচের দিকে কাজ করে । ইহা রোলারের ওজন বৃদ্ধি করে । H উপাংশ অনুভূমিক দিকে ক্রিয়া করে । এই উপাংশটি রোলারকে সামনে নিয়ে যেতে সাহায্য করে । রোলার ঠেলা কষ্টকর কারণ উলম্ব উপাংশটি অভিকর্ষের দিকে কাজ করে ।

  রোলার টানা -

           

 এক্ষেত্রে OA  অভিমুখে বল প্রয়োগ করা হয় । এর অনুভূমিক ও উলম্ব উপাংশ দুটি  H এবং V | রোলার টানার সময় উলম্ব উপাংশটি উপরের দিকে কাজ করে । ইহা রোলারের ওজন কমাতে সাহায্য করে ।সুতরাং রোলার টানা অপেক্ষাকৃত সহজ ।

নিউটনের দ্বিতীয় গতিসূত্র :

বিবৃতি - কোনো বস্তুর ভরবেগ পরিবর্তনের হার বস্তুটির ওপর প্রযুক্ত বলের সমানুপাতিক । প্রযুক্ত বল যে দিকে ক্রিয়া করে ভরবেগের পরিবর্তনও সেই দিকে হয় ।

বল প্রয়োগের ফলে ভরবেগের পরিবর্তন ঘটে , অর্থাৎ বস্তুর বেগের পরিবর্তন হয় ।আর বেগের পরিবর্তনের অর্থ হল বস্তুর মধ্যে ত্বরণ দেখা যায় ।

পরীক্ষাগত ভাবে নিউটন দেখান যে নিৰ্দিষ্ট ভরের বস্তুর প্রযুক্ত বাহ্যিক বল(F) বেগের পরিবর্তন বা উৎপন্ন ত্বরণের(a) সমানুপাতিক । অর্থাৎ 

  a ∝ F ( যখন ভর ( m) = ধ্রুবক )

আবার যখন সমপরিমাণ বল বিভিন্ন ভরের বস্তুর ওপর প্রয়োগ করা হয় তখন ভর কম হলে ত্বরণ বেশি হয় ,আর ভর বেশি হলে ত্বরণ কম হয় । অর্থাৎ ত্বরণ ভরের সঙ্গে ব্যাস্তানুপাতে পরিবর্তণ হয় ।

∴ a ∝ 1/m (যখন  F ধ্রুবক )

উপরের দুই সমীকরণ থেকে লেখা যায় -

  a ∝ F/m ( যখন  F এবং m উভয়ই পরিবর্তনশীল )

∴ a = K x F/m ( K একটি ধ্রুবক ,এর মান একক বলের ধারণার উপর নির্ভরশীল )

⇒ F = K am ...(.1)

একক ভরের বস্তুর উপর যে বল ক্রিয়া করে একক ত্বরণ সৃষ্টি করে তাকে একক বল বলা হলে K = 1 হবে । অর্থাৎ  1 = K x 1 x 1 

⇒ K = 1 

( 1) নম্বর সমকরণে   K = 1 বসিয়ে পাই ,

 F = a m 

অর্থাৎ  প্রযুক্ত বল  = বস্তুর ভর х ত্বরণ , এটি হল নিউটনের দ্বিতীয় সূত্রের গাণিতিক রূপ ।

নিউটনের দ্বিতীয় গতিসূত্র থেকে প্রথম গতিসূত্র প্রতিষ্ঠা :

⇒ দ্বিতীয় সূত্রের গাণিতিক সমীকরণটি , F = ma .

বস্তুর ওপর বাহ্যিক বল প্রয়োগ না হলে ,  F = 0 

⇒ ma = 0 

অর্থাৎ   a = 0 (  বস্তুর ভর , m ≠ 0 )

⇒ (v-u)/t = 0 

বা  v - u = 0 

∴ v = u 

⇒ অন্তিম বেগ = প্রাথমিক বেগ 

অর্থাৎ বস্তুটি সমবেগে চলছে ।

আর  যদি  u = 0 হয় , বস্তুটি স্থির থাকবে ।

অর্থাৎ , বল প্রয়োগ না করলে স্থির বস্তু চিরকাল স্থির থাকবে আর সচল বস্তু চিরকাল সমবেগে সরলরেখায় গতি বজায় রাখবে । এটাই নিউটনের প্রথম গতিসূত্র ।

বস্তুর ভরই জাড্যের পরিমাপ :

দ্বিতীয় গতিসূত্র থেকে পাই ,

F = maতাকে ⇒ a = F/m

⇒ a ∝ 1/m  ( F = স্থির বা ধ্রুবক )

অর্থাৎ উৎপন্ন ত্বরণ বস্তুর ভরের সঙ্গে ব্যাস্তানুপাতে পরিবর্তিত হয় ।

⇒ ভর বেশি হলে ত্বরণ কম হবে , ভর কম হলে ত্বরণ বেশি হবে ।

অর্থাৎ ভরই হল বস্তুর জড়তার পরিমাপ ।

বলের একক :

বলের দুই প্রকার একক আছে - ১) পরম একক  ২) অভিকর্ষজ একক ।

বলের পরম একক(Absoluteunit of force) : 

CGS পদ্ধতিতে বলের একক ডাইন ।

ডাইন - 1 গ্রাম ভরের বস্তুর উপর যে বল ক্রিয়া করলে বলের অভিমুখে 1 সেমি /সে² ত্বরণ সৃষ্টি করে 

তাকে 1 ডাই ন বলে ।

SI পদ্ধতিতে বলের একক নিউটন ।

নিউটন - 1 কিলোগ্রাম ভরের বস্তুর উপর যে বল ক্রিয়া করলে বলের অভিমুখে 1 m/s² ত্বরণ সৃষ্টি হয় তাকে  1 নিউটন বল বলে ।

নিউটন ও ডাইনের মধ্যে সম্পর্ক :

1 নিউটন = 1 kg х1m/s²

               = 1000 g х 100 cm/s²

               = 10⁵ g. cm/s²

              = 10⁵ ডাইন 

বলের একটি বড় একক হল মেগা ডাইন । 1 মেগা ডাইন  = 10⁶ ডাইন  ।

বলের অভিকর্ষীয় একক :

CGS পদ্ধতিতে বলের অভিকর্ষীয় একক গ্রাম-ভার ।

1 গ্রাম-ভার - এক গ্রাম ভরের কোনো বস্তুকে পৃথিবী যে বলে নিজের কেন্দ্রের দিকে আকর্ষণ করে তাকে এক গ্রাম-ভার বল বলে ।

1 গ্রাম- ভার  =  1 গ্রাম x g সেমি /সে²

                       = g ডাইন 

                      = 981 ডাইন ।( g = 981 cm/s²)

SI পদ্ধতিতে বলের অভিকর্ষজ একক কিলোগ্রাম-ভার ।

1 কিলোগ্রাম-ভার = 1 কিলোগ্রাম ভরের কোনো বস্তুকে পৃথিবী যে বল দ্বারা কেন্দ্রের দিকে আকর্ষণ করে তাকে এক কিলোগ্রাম-ভার বল বলে ।

 1 কিলোগ্রাম-ভার =  1 kg х g m/s²

                               = g Newton 

                              = 9.81 Newton( g = 9.81 m/s² )

বলের মাত্রা = [ ভর ] х[ত্বরণ ] = [M] x[LT⁻²] = [MLT⁻²]

গাণিতিক উদাহরণ :

1. 150 গ্রাম ভরেরবস্তুর উপর 450 ডাইন বল প্রয়োগ করা হলে কত ত্বরণ সৃষ্টি হবে ?

সমাধান - বস্তুর ভর , m = 150 গ্রাম , বস্তুর উপর প্রযুক্ত বল ,F = 450 ডাইন । ত্বরণ , a = ?

নিউটনের দ্বিতীয় গতি সুত্রে(F = ma ) মানগুলি বসিয়ে পাই ,

450 = 150 x a 

⇒ a = 450/150 = 3 সেমি/সে² 

2. 1 kg ভরের বস্তুর উপর 3 N বল 10 s ধরে ক্রিয়া করলে স্থির অবস্থা থেকে  কত বেগ লাভ করবে ?

সমাধান - বস্তুর ভর , m = 1 kg. প্রযুক্ত বল , F= 3 N

∴ ত্বরণ , a = F/a = 3/1 = 3 m/s² 

এখন ,  v = u + a t থেকে পাই ,

     v = 0 + 3 x 10  =30 m/s

∴ বস্তুটি 30 m/s বেগ লাভ করবে ।

নিউটনের তৃতীয় গতিসূত্র (Newton's third law).

প্রত্যেক ক্রিয়ার একটি সমান ও বিপরীত প্রতিক্রিয়া থাকে ।

ক্রিয়া  ও প্রতিক্রিয়া :

যখন একটি বস্তু অপর কোনো বস্তুর উপর বল প্রয়োগ করে তখন ওই বলটিকে ক্রিয়া বলে । তৃতীয় সূত্র  অনুসারে  দ্বিতীয় বস্তুটি প্রথম  বস্তুর উপর একটি  সমান বিপরীত মুখী  বল প্রয়োগ করে । ওই  বলটিকে প্রতিক্রিয়া  বলে ।

ক্রিয়া ও প্রতিক্রিয়ার বৈশিষ্ট্য :
1) প্রকৃতিতে একক বিচ্ছিন্ন বলের কোনো অস্তিত্ব নাই ।বল সর্বদা ক্রিয়া ও প্রতিক্রিয়া রূপে দুটি ভিন্ন বস্তুর উপর কাজ করে । 2) ক্রিয়া যতক্ষন কাজ করে প্রতিক্রিয়াও ততক্ষন কাজ করে ।

3) ক্রিয়া ও প্রতিক্রিয়ার দ্বারা সাম্য প্রতিষ্টিত হয় না ,কারণ ক্রিয়া ,প্রতিক্রিয়া দুটি ভিন্ন বস্তুর উপর কাজ করে ।সাম্য প্রতিষ্টার জন্য দুই সমপরিমাণ বিপরীত মুখী বল একই বস্তুর উপর ক্রিয়া করা দরকার ।

তৃতীয় সূত্রের উদাহরণ :

পৃথিবী ও সূর্যের মধ্যে আকর্ষণ বল ক্রিয়া - প্রতিক্রিয়ার একটি উদাহরণ ।পৃথিবী এবং সূর্য্য যে বল দ্বারা পরস্পরকে আকর্ষণ করে তা পরস্পর সমান এবং বিপরীত মুখী ।

সূর্যের দ্বারা পৃথিবীর উপর প্রযুক্ত বল Fg হলে পৃথিবীর দ্বারা সূর্যের উপর - Fg হবে ।

অনুভূমিক তলে হাঁটা :
একজন লোক যখন মাটির উপর হেঁটে যায় তখন সে মাটির উপর তীর্যক ভাবে বল প্রয়োগ করে (ক্রিয়া ) মাটিও লোকটির উপর সমান ও বিপরীত মুখী বল প্রয়োগ করে ।এটিকে প্রতিক্রিয়া বলে । এই প্রতিক্রিয়া বলের অনুভূমিক উপাংশ লোকটিকে সামনের দিকে নিয়ে যেতে সাহায্য করে ।

       

বিভিন্ন ধরনের বল :

প্রকৃতি ও ধর্মের ভিত্তিতে আমরা বলকে দুই ভাগে ভাগ করতে পারি ।

1) স্পর্শজনিত বা সংযোগ বল  2) ক্ষেত্রজনিত বা অসংযোগ বল ।

1) স্পর্শজনিত বা সংযোগ বল( Contact Force):

দুটি বস্তু পরস্পর সংস্পর্শে থাকাকালীন তাদের পারস্পরিক ক্রিয়ায় যে কাজ করে তাকে সংযোগ বল বলে । যেমন- ঘর্ষণ ,টান , লম্ব প্রতিক্রিয়া  ইত্যাদি ।

2) ক্ষেত্রজনিত বা অসংযোগ বল(Field force or non contact force):

দুটি বস্তু সংস্পর্শে না থেকেও ওদের মধ্যে যখন ক্রিয়া  প্রতিক্রিয়া কাজ করে থাকে সেই বলকে অসংযোগ বল বলে । উদাহরণ - মহাকর্ষীয় বল , তড়িৎ বল ,চুম্বকীয় বল  ইত্যাদি ।

বলের ঘাত ও ঘাত বল (Impulse of force and Impulsive force )

বলের ঘাত :

কোনো বস্তুর উপর যখন একটি নিৰ্দিষ্ট মানের বল কিছু সময় ধরে ক্রিয়া করে তখন প্রযুক্ত বল ও তার ক্রিয়াকালের গুণফলকে বলের ঘাত বলে । বলের ঘাতের CGS একক dyne-s | SI একক হল N-s |

ঘাতের মাত্রা  = বলের মাত্রা х সময়ের মাত্রা  = [MLT⁻²] [ T] = [MLT⁻¹]

ঘাত বল :

যখন কোনো বৃহৎ মানের বলের ক্রিয়াকাল খুব হয় , কিন্তু ভরবেগের নিৰ্দিষ্ট পরিবর্তন ঘটায় এবং বলের ক্রিয়াকালের সময় বস্তুর উপেক্ষণীয় হয় সেই বলকে ঘাত বল বলে ।উদাহরণ - ক্রিকেট ব্যাট দিয়ে ক্রিকেট বলকে মারলে এক্ষেত্রে প্রযুক্ত বলকে ঘাত বল বলে । হাতুড়ি দিয়ে পেরেক পোঁতার সময় হাতুড়ি দ্বারা পেরেকের উপর প্রযুক্ত বল হল ঘাত বল ।,ফুটবলে কিক মারার সময় পা দিয়ে ফুটবলে বল প্রয়োগ হল ঘাত বল ।

      ঘাত বল  ও বলের ঘাতের মধ্যে পার্থক্য :

ঘাত বল	বলের ঘাত
1.ঘাত বল একটি বৃহৎ মানের ক্ষণস্থায়ী বল	1.বলের ঘাত বল ও বলের ক্রিয়াকালের গুনফল
2. ঘাত বলের মাত্রা [MLT⁻²]	2. বলের ঘাতের মাত্রা [MLT⁻¹]
3.ঘাত বল ভরবেগের পরিবর্তন দ্বারা মাপা হয় অর্থাৎ  F x t দ্বারা মাপা হয়	3.বলের ঘাতের বেলায় প্রযুক্ত বল F = ma সমীকরণ দ্বারা মাপা হয় ।
4.এর প্রভাবে অল্প সময়ে বৃহৎ ত্বরণ সৃষ্টি হয় ।	4.বলের ঘাতের প্রভাবে ভরবেগের পরিবর্তন ঘটে ।
5.ঘাত বল হল কারণ ।	5.বলের ঘাত হল ফল ।

রৈখিক  ভরবেগ (Linear Momentum):

একটি টেনিস বল  ও একটি লোহার বল একই বেগে কোনো দেওয়ালে আঘাত করলে লোহার বলটি দেওয়ালে বেশি বল প্রয়োগ করবে ,টেনিস বলটি দেওয়ালে কম বল প্রয়োগ করবে কারণ লোহার বলটির ভর বেশি । অর্থাৎ প্রযুক্ত বল ভরের সমানুপাতিক ।

আবার যদি একই ভরের দুটি লোহার বল যদি বিভিন্ন বেগে কোনো দেওয়ালে ধাক্কা লাগে তাহলে যে বলটির বেগ বেশি সেটি দেওয়ালে অধিক বল প্রয়োগ করবে । অর্থাৎ এক্ষেত্রে প্রযুক্ত বল বেগের সঙ্গে সমানুপাতি ।

সুতরাং লক্ষ্য করা যায় যে কোনো বস্তুর গতীয় আচরণ উহার ভর ও বেগের উপর নির্ভর করে । একটি বস্তু অন্য কোনো বস্তুর উপর কতটা বল প্রয়োগ করবে তা বস্তুটির  ভর ও বেগের উপর নির্ভরশীল ।

রৈখিক ভরবেগের সংগা :

ভর ও বেগের সমন্বয়ে কোনো গতিশীল বস্তুর মধ্যে নূতন গতীয় ধর্মের সৃষ্টি হয় তাকে রৈখিক ভরবেগ বলে ।ভর ও বেগের গুনফল দ্বারা ভরবেগ পরিমাপ করা হয় ।

অর্থাৎ ভরবেগ = ভর x  বেগ । 

ভরবেগ একটি ভেক্টর রাশি ,কারণ এর অভিমুখ আছে । বেগের অভিমুখীই হল ভরবেগের অভিমুখ ।

ভরবেগের মাত্রা = ভরের মাত্রা x বেগের মাত্রা   = [M ] x [LT⁻¹]  = [MLT⁻¹]

ভরবেগের একক  - CGS পদ্ধতিতে একক গ্রাম-সেমি/সে 

     SI পদ্ধতিতে একক  কিলোগ্রাম- মিটার/সেকেন্ড  ।

ভরবেগের ধারণা থেকে নিউটনের গতিসূত্র :

মনে করি বালিভর্তি একটি গাড়ি সমবেগে চলছে । গাড়ির তলায় একটি ছিদ্র দিয়ে সমহারে বালি পড়ছে ,এতে গাড়ির ভর ক্রমশ কমে যাচ্ছে । ফলস্বরূপ গাড়ির বেগও সমহারে বেড়ে যাবে ।এক্ষেত্রে বাহিরের থেকে কোনো বল প্রয়োগ না করা সত্ত্বেও ভরের পরিবর্তনের জন্যে বেগের পরিবর্তন হচ্ছে । এই ক্ষেত্রে F = ma সমকরণটি প্রয়োগ করা সম্ভব নয় । কারণ এখানে ভর m  পরিবর্তন হয়ে যাচ্ছে । এইসব ক্ষেত্রে ব্যাখ্যার জন্য ভরবেগের ধারণার প্রয়োজন ।

রৈখিক ভরবেগের ধারণা থেকে  F = ma সমীকরণ প্রতিষ্ঠা :

        

ধরা যাক m ভরের একটি বস্তুর প্রাথমিক বেগ u , বস্তুটির উপর F বল t সময় ধরে প্রয়োগ করায় পরিবর্তিত বেগ হয়  v |

এক্ষেত্রে বস্তুটির প্রাথমিক ভরবেগ = mu ,অন্তিম ভরবেগ = mv 

∴ t সময়ে ভরবেগের পরিবর্তন = mv - mu 

⇒ ভরবেগ পরিবর্তনের হার = (mv - mu)/t= m(v -u)/t  = ma  [∵ (v - u)/t = ত্বরণ = a ]

দ্বিতীয় গতিসূত্র অনুসারে প্রযুক্ত বল ভরবেগ পরিবর্তনের হারের সঙ্গে সমানুপাতি 

∴ প্রযুক্ত বল ,F ∝ ma

বা  F = K ma ( K = ধ্রুবক )

এখন যদি m = 1 , a = 1 হলে  F = 1 হয়  তাহলে K = 1 হবে ।

∴ F = ma ,এটাই নিউটনের দ্বিতীয় গতিসূত্র ।

রৈখিক ভরবেগের সংরক্ষণ সূত্র :
বাহিরের থেকে কোনো বল প্রযুক্ত না হলে কতকগুলি বস্তুর মধ্যে ক্রিয়া প্রতিক্রিয়ার দরুন যে কোনো নিৰ্দিষ্ট দিকে বস্তুগুলির মোট ভরবেগ অপরিবর্তিত থাকে ।

ব্যাখ্যা - ধরা যাক m₁ ও m₂ ভরের দুটি বস্তুকণা যথাক্রমে u₁ ও u₂ বেগনিয়ে চলছে । এদের মধ্যে সংঘর্ষ হল । সংঘর্ষের পরে এদের বেগ যথাক্রমে v₁ ও v₂ হয় ।রৈখিক ভরবেগের সংরক্ষন সূত্র থেকে লেখা যায় - সংঘর্ষের পূর্বে মোট ভরবেগ  = সংঘর্ষের পরে মোট ভরবেগ ।

⇒ m₁u₁ + m₂u₂ =m₁v₁ + m₂v₂

নিউটনের তৃতীয় গতিসূত্র থেকে ভরবেগের সংরক্ষণ সূত্রের ব্যাখ্যা ;

উপরের চিত্র থেকে লেখা যায় প্রথম বস্তুর ভরবেগের পরিবর্তন = m₁v₁ - m₁u₁

দ্বিতীয় বস্তুর ভরবেগের পরিবর্তন = m₂v₂ -  m₂u₂
সংঘাতের ফলে প্রথম বস্তুর উপর প্রযুক্ত বল =,F₁ = ( m₁v₁ - m₁u₁)/t [ যেহেতু  প্রযুক্ত বল = ভরবেগ পরিবর্তনের হার , t = সংঘর্ষের ক্রিয়াকাল ।

দ্বিতীয় বস্তুর উপর প্রযুক্ত বল  = F₂ = (m₂v₂ -  m₂u₂)/t 

তৃতীয় সূত্রানুসারে ক্রিয়া ও প্রতিক্রিয়া পরস্পর সমান ও বিপরীত মুখী 

⇒ F₁ = - F₂

বা  ( m₁v₁ - m₁u₁)/t  = -  (m₂v₂ -  m₂u₂)/t

বা ,m₁v₁ + m₂v₂ = m₁u₁ + m₂u₂

অর্থাৎ সংঘাতের পরে বস্তুদুটির মোট রৈখিক ভরবেগ  = সংঘাতের আগে বস্তুদুটির মোট রৈখিক ভরবেগ ।

সুতরাং বস্তু দুটির মোটরৈখিক  ভরবেগ ধ্রুবক ।

রৈখিক ভরবেগের সংরক্ষণ সূত্রের প্রয়োগ ;

বন্দুক থেকে গুলি ছোড়ার সময় ভরবেগের সংরক্ষণ সূত্রের প্রয়োগ -

গুলি ছোড়ার সময় গুলি যেভরবেগ নিয়ে বেরিয়ে যায় বন্দুকও সেই একই ভরবেগ নিয়েপিছু হটে । ভরবেগের সংরক্ষণের জন্য এমন হয় ।

মনেকরি গুলির ভর = m , বন্দুকের ভর = M 

গুলির বেগ = v , বন্দুকের ভাগ = V 

ভরবেগের সংরক্ষণ নীতি থেকে ,

mv + MV = 0 

বা , V = -  mv/M, ঋণাত্মক চিহ্ন বন্দুক ও গুলির বেগ পরস্পর বিপরীত নিৰ্দেশ করছে । ∵ m/M <<1 হয় ,বন্দুকের বেগ  তুলনায় অনেক কম হয় ।

হোসপাইপ দিয়ে জল প্রবাহিত হওয়ার সময় হাতে ধরে রাখা অসুবিধাজনক :

হোসপাইপ দিয়ে যখন তীব্র বেগে জল বেরিয়ে আসে তখন রৈখিক ভরবেগের সংরক্ষণ নীতি অনুযায়ী হোসপাইপটিও তীব্র গতি নিয়ে   পিছনের দিকে যেতেচায় । ফলে পাইপটিকে ধরে রাখা অসুবিধাজনক  হয় ।

রকেটের ক্ষেত্রে রৈখিক ভরবেগের সংরক্ষণ নীতি :

রকেটের জ্বালানি দহনের ফলে উৎপন্ন গ্যাস পেছনের একটি সরু ছিদ্র দিয়ে তীব্র বেগে নির্গত হয় ,ফলস্বরূপ রকেট উপরের দিকে তীব্র গতিশীল হয় । ভরবেগের সংরক্ষণ নীতি অনুসারে লেখা যায় - রকেটের ভরবেগ + নির্গত গ্যাসের ভরবেগ  = ০ 

∴ রকেটের ভরবেগ = - নির্গত গ্যাসের ভরবেগ ।

                                               :অনুশীলনী :

                                      বাম স্তম্ভের সঙ্গে ডান স্তম্ভ মিলাও 

বাম স্তম্ভ	ডান স্তম্ভ
i) নিউটনের প্রথম গতিসূত্র	i) মহাকর্ষ
ii) রৈখিক ভরবেগ	ii) ঘর্ষণ বল
iii) সংযোগ বল	iii) ভরবেগ
iv) নিউটনের দ্বিতীয় গতিসূত্র	iv) বলের সংজ্ঞা
v) অসংযোগ বল	v) বলের সংজ্ঞা

সঠিক উত্তরটি নির্বাচন কর (MCQ): https://forms.gle/CdrSDtScacESAWhG9

1.বলের মাত্রীয় সংকেত হল - 

A) MLT⁻¹ B) MLT⁻² C) ML⁻¹T⁻²  D) M²LT⁻¹

2, অভিকর্ষের অধীনে অবাধে পতনশীল বস্তু এক সেকেন্ডে আবারোহান করে তা হল - 

A) g  B) 2g  C) g/2  D) 3g

3. ৰৈখিক ভর বেগের SI একক 

A) kgms⁻¹  B) kgcms⁻¹  C) gcms⁻¹  D) gms⁻¹

4.নিজের অক্ষ সাপেক্ষে পৃথিবীর গতি হল  -

A) ঘুর্ণন গতি  B) চলন গতি  C) বৃত্তীয় গতি  D) কোনোটিই নয় 

5.একটি বস্তুর সরণ s এবং অতিক্রান্ত দূরত্ব d হলে -

A) d = s  B) d ≥ s  C) d ≤ s D) কোনোটিই নয় 

6.কোনো বলের দুটি সম কৌণিক উপাংশ 3N এবং 4N হলে বলের মান -

A) 7N  B) 8N  C) 6N  D) 5N

7.একটি বস্তু সম দ্রুতিতে গতিশীল কণাটির গতিবেগ --

A) পরিবর্তনশীল  B) পরিবর্তনশীল হতেও পারে নাও হতে পারে  C) ধ্রুবক   D) কোনোটিই নয় 

8.রকেটের গতি যে সংরক্ষণ নীতির প্রতিষ্ঠিত তা হল --

A) ভর  B) রৈখিক ভরবেগ  C) বল   D) গতিশক্তি 

9.একটি বস্তুর প্রাথমিক বেগ শুন্য এবং ত্বরণ 2 cm/s² ,4 s পরে বস্তুটির গতিবেগ হবে --

A) 4 সেমি /সে  B) 16 সেমি /সে  C) 2 সেমি /সে  D) 8 সেমি /সে 

10. কোনো বস্তুর ওপর স্থির মানের বল প্রয়োগ করতে থাকলে বস্তুটির  - 

A) সমান ভরবেগ থাকবে  B) সম ত্বরণ থাকবে  C) সম দ্রুতি থাকবে  D) সমবেগ থাকবে 

11.একটি কণা r ব্যাসার্ধের একটি বৃত্তাকার পথের অর্ধেক অতিক্রম করলে এর সরণ হবে - 

A) 2πr B) r  C) 2r  D) πr²      

Units and Measurement(একক ও পরিমাপ )

Units and Measurement(একক ও পরিমাপ )

প্রাকৃতিক রাশি (Physical Quantity):পরিমাপ যোগ্য যে কোনো প্রাকৃতিক বিষয়কেই  প্রাকৃতিক রাশি বা  ভৌতরাশি বলে ।যেমন দৈর্ঘ্য ,ভর ,সময় ,তাপমাত্রা এবং গতিবেগ  ইত্যাদি ।  ( Any natural subject that can be measured directly or indirectly is known as physical quantity. Example-Length,Mass,Time,Temperature,Velocity etc)

দুই প্রকারের  ভৌত বা  প্রাকৃতিক রাশি হয়  - 1 . স্কেলার রাশি  2.  ভেক্টর রাশি (Physical Quantity is of  two types- 1) Scalar Quantity 2) Vector Quantity.)
1)স্কেলার রাশি ( Scalar quantity)-যে সকল রাশির  শুধু  মান আছে  কিন্তু কোনো অভিমুখ নেই  তাদের স্কেলার রাশি  বলে ।যেমন  - দৈর্ঘ্য ,ভর , সময়  ও ঘনত্ব  ইত্যাদি । (Quantities that have only magnitudes but no directions are known as scalar quantity.Examples - Length,Mass,Time , Density etc.)
2)ভেক্টর রাশি(Vector Quantity) - যে সকল রাশির মান ও অভিমুখ দুইই আছে  তাদের ভেক্টর রাশি বলে ।যেমন - সরণ , বেগ ,ত্বরণ এবং বল  ইত্যাদি ।(Quantities having both magnitudes and directions and added according to vector addition rules are known as vector quantity. Examples- Displacement,Velocity,Acceleration Force etc.)

ভেক্টর রাশির জ্যামিতিক প্রকাশ (Geometrical Expression of Vectors)- যেহেতু এই রাশির মান  ও দিক দুটোই আছে  এই রাশি  তীর চিহ্ন যুক্ত সরলরেখা দ্বারা এবং মোটা ইংরেজী অক্ষরের দ্বারা প্রকাশ করা হয় ।যেমন AB  বা  ⟶(Since it  has both magnitude and direction it is represented by bold English letter with a overhead directed line segment. Such as AB etc.)

 

                 
                                                স্কেলার  ও ভেক্টর রাশির পার্থক্য 

স্কেলার রাশি	ভেক্টর রাশি
1.স্কেলার রাশির মান আছে ,অভিমুখ নেই ।	1.ভেক্টর রাশির মান ও অভিমুখ দুটিই আছে ।
2.দুটি স্কেলার রাশির গুনফল সর্বদা স্কেলার রাশি  হয় ।	2'.দুটি ভেক্টর রাশির গুনফল স্কেলার বা ভেক্টর দুইই হতে পারে ।
3.এক জাতীয় স্কেলার রাশির যোগ বা বিয়োগ বীজগণিতের সাধারণ নিয়ম অনুসারে হয় ।	3.অভিমুখ থাকায় এক জাতীয় ভেক্টর রাশির যোগ বা বিয়োগ সাধারণ বীজগণিতের নিয়ম অনুসারে হয় না ।
4. একক যুক্ত বা একক হীন সংখ্যার দ্বারা স্কেলার রাশি প্রকাশ করা হয় ।	4.কিন্তু ভেক্টর রাশিকে একটি তীরচিহ্ন যুক্ত সরল রেখাংশ দ্বারা প্রকাশ করা যায় ।

প্রাকৃতিক রাশির একক ( Units of Physical Quantities) -- কোনো রাশি মাপতে হলে ওই রাশিটির একটি নিৰ্দিষ্ট ও সুবিধাজনক পরিমাণকে প্রমাণ ধরে প্রদত্ত রাশিটির পরিমান ওই প্রমাণ মানের যত গুণ তা মাপা হয়  ।ওই প্রমাণ মানটিকে ওই রাশির একক বলে ।(When a physical quantity is measured a suitable amount of the quantity is taken standard value and the quantity is measured by comparison with the predetermined  standard value.This standard value is called unit of the  quantity)

এককের প্রয়োজনীয়তা (Utility of Units )- একক ছাড়া কোনো ভৌত রাশি পরিমাপ করা সম্ভব নয় ।ভৌত রাশির সঠিক পরিমাপের জন্য এককের প্রয়োজন হয় ।একক ছাড়া শুধু  সংখ্যা  দ্বারা কোনো সম্পূর্ণ অর্থ প্রকাশ পায় না ।বিভিন্ন ভৌত রাশির স্বাতন্ত্রতা বুঝানোর জন্যে এককের প্রয়োজন হয় । যেমন  - 10 গ্রাম  ও 10 মিটার  দ্বারা আমরা ভর ও দৈর্ঘ্য নামে দুটি রাশিকে বোঝানো হয় ।বিভিন্ন ভৌত রাশির মধ্যেসম্পর্ক স্থাপনের জন্য এককের প্রয়োজন ।(It is not possible to measure physical quantity without  units. Physical quantity is expressed in numerical value with units.Physical quantity with units maintain its  difference from other quantity.When relation between  quantities are needed to be  established units are taken into consideration.)
প্রাথমিক বা মৌলিক একক  এবং লব্ধ একক ( Fundamental and Derived Units)-
পদার্থবিদ্যায় এককের সংখ্যা প্রচুর । বিভিন্ন এককগুলিকে শ্রেণিবদ্ধ করার প্রয়োজনীয়তা আছে । এককগুলিকে  সাধারণত দুটি শ্রেণীতে বিভক্ত করা হয় ।(There are so many units in Physics.We need to classify them.We can classify them as two types) --
1)প্রাথমিক একক ( Fundamental Unit )2) লব্ধ একক (Derived Unit).)প্রাথমিক একক (Fundamental Units) - যে ভৌত একক  পরস্পরের  উপর  নির্ভরশীল নয় এবং যে  রাশিগুলির এককের সাহায্যে অন্যান্য রাশির একক গঠন করা যায় তাদের  প্রাথমিক বা  মৌলিক একক বলে ।যেমন - দৈর্ঘ্য ,ভর ,সময় ,তাপমাত্রা ,তড়িৎ প্রবাহ মাত্রা ,দীপন প্রাবল্য ও পদার্থের পরিমাণ,  - এই সাত টি রাশির একক স্বাধীন এককগুলিকে মৌলিক বা প্রাথমিক একক বলে ।( Units of those physical quantities that are independent and have no dependency with one another are called Fundamental Units.In CGS System these are taken as units of Length,Mass and Time.But in SI System these are units of Length, Mass, Time , Electric current,Temperature,,Amount of matter,Intensity of light.
Fundamental units are limited in numbers.)
2)লব্ধ একক (Derived units)- যে ভৌত রাশিগুলির একক এক  বা একাধিক মৌলিক এককের সাহায্যে গঠিত  হয়  সেই সব এককগুলিকে লব্ধ একক বলে ।যেমন - বেগ ,ত্বরণ ,ভরবেগ ,বল ও কাজ  ইত্যাদি এর  একক হল লব্ধ একক ।(Units that are derived from fundamental units are known as Derived units.These are units of Velocity,acceleration,momentum,Force,Work etc.There are so many derived units)

বেগের একক লব্ধ .একক কেন ?

বেগ  = সরণ / সময়  । অর্থাৎ বেগের একক  = সরণের একক /সময়ের একক । সুতরাং বেগের একক দৈর্ঘ্য ও সময়ের এককের ওপর নির্ভরশীল । এজন্য বেগের একক লব্ধ একক ।
এককের বিভিন্নপদ্ধতি ( Different System of Units) -আগেকার দিনে বিজ্ঞানীরা পরিমাপের জন্য  তিন প্রকারের পদ্ধতি ব্যবহার করতেন । যেমন CGS পদ্ধতি ,FPS , MKS  পদ্ধতি ।কিন্তু বর্তমানে দুই প্রকারের পরিমাপের পদ্ধতি প্রচলিত CGS এবং  SI(System of International Units)পদ্ধতি (In earlier time scientist used three systems of units.1) CGS System 2) FPS System 3) MKS System.But now Two system of units are in use 1) CGS 2) SI System In CGS System unit of length -(cm),of mass - Gram(g) and unit of time -Second(s).

                                                     CGS পদ্ধতি      

রাশি	একক	প্রতীক
1.দৈর্ঘ্য	সেমি	cm
2.ভর	গ্রাম	g
3.সময়		s

In SI System following are the  fundamental units.

                                  SI পদ্ধ তিতে বিভিন্ন একক              

রাশি		প্রতীক
1. দৈর্ঘ্য	মিটার	m
2.ভর	কিলোগ্রাম	kg
3. সময়	সেকেন্ড	s
4.তড়িৎ প্রবাহ মাত্রা	এম্পিয়ার	A
5. উস্নতা	কেলভিন	K
6. আলোর দীপ্তি	ক্যান্ডেলা	cd
7.পদার্থের পরিমাণ	মোল	mol

কোণ (Angle) - রেডিয়ান (radian (rd))(এটি একটি পরিপূরক একক )

SI পদ্ধতিতে কয়েকটি লব্ধ এককের নাম  এবং প্রতীক - 

     

রাশি	একক	প্রতীক
1.আয়তন	ঘনমিটার	m³
2.ত্বরণ	মি /সে²	m/s²
3. বল	নিউটন	N
4.ভরবেগ	কিলোগ্রাম-মিটার	Kg-m
5.কার্য্য বা শক্তি	জুল	J
6.ক্ষমতা	ওয়াট	W
7.চাপ	পাস্কাল	Pa
8.তড়িতাধান	কুলম্ব	C
9.তড়িৎবিভব	ভোল্ট	V
10.রোধ	ওহম	ᘯ
11.কম্পাঙ্ক	হার্টজ	Hz
12.ঘনত্ব	কিগ্র্যা /মি³	kg m⁻³
13.গাঢ়ত্ব	মোল/মি³	mol m⁻³

আরো অধিক জানার জন্য নীচের লিংক টি ওপেন কর -

   https://wordpress.com/block-editor/post/physicsproblemsdotcom.wordpress.com/33

একক হীন  রাশি (Unitless Physical Quantity)-যে সমস্ত প্রাকৃতিক রাশিকে দুটি সমজাতীয় রাশির অনুপাত আকারে প্রকাশ করা যায় তাদের কোনো একক থাকে না । এদের একক হীন রাশি বলে ।(If a physical quantity is defined as the ratio of two similar quantity then it is called unitless

 quantity).

উদাহরণ (Example )- 1) কোনো মৌলের পারমানবিক ওজন = মৌলের একটি পরমাণুর ভর/ একটি C¹²  পরমাণুর ভরের 1/12 অংশ ।(Atomic weight = Mass of an atom of an element /Mass of a single hydrogen atom.) 2) আপেক্ষিক গুরুত্ব ( Specific Gravity) = কোনো বস্তুর ভর /4ºC উস্নতায় সম আয়তন  জলের ভর (Mass of an object/ Mass of equal volume of water at 4 degree C.)

একই ভাবে বলা যায় আনবিক ভর ,বিকৃতি ,আপেক্ষিক আর্দ্রতার কোনো একক নাই ।

বিভিন্ন ছোটো ও বড় একক বোঝাতে বিভিন্ন উপসর্গের(Prefix) প্রয়োগ ।

CGS ও SI পদ্ধতিতে অনেক ক্ষেত্রে দৈর্ঘ্য ,ভর  ও সময়ের পরিমাপের ক্ষেত্রে নিম্ন লিখিত উপসর্গ গুলি ব্যবহার করা হয় ।

ছোটো একক প্রকাশ করার জন্য ব্যবহৃত উপসর্গ :

উপসর্গ	ভগ্নাংশ	চিহ্ন
ডেসি (deci)	10⁻¹	d
সেন্টি  (centi)	10⁻²	c
মিলি (mili)	10⁻³	m
মাইক্রো (micro)	10⁻⁶	μ
ন্যানো nano)	10⁻⁹	n
পিকো(pico)	10⁻¹²	p
ফেমটো(femto)	10⁻¹⁵	f
অটো(atto)	10⁻¹⁸	a

 বড় একক প্রকাশ করার জন্য ব্যবহৃত উপসর্গ 

উপসর্গ	গুণিতক	চিহ্ন
ডেকা	10	da
হেক্টো	10²	h
কিলো	10³	k
মেগা	10⁶	M
গিগা	10⁹	G
টেরা	10¹²	T
পেটা	10¹⁵	p
এক্সা	10¹⁸	E

দৈর্ঘ্য  ভর ও সময়ের এককের আধুনিক ধারণা (Modern concept of units of length,mass and time):

দৈর্ঘ্যের SI একক হল মিটার (Unit of length in SI System ie. metre(m) )-শুন্য মাধ্যমে আলো 1/299792458  সেকেন্ডে যে দূরত্ব অতিক্রম করে তাকে এক মিটার বলে ।
SI পদ্ধতিতে ভরের একক- কিলোগ্রাম  (Unit of mass in SI System - kilogramme(kg))--ফ্রান্সের  প্যারিসে ইন্টারন্যাশনাল ব্যুরো অফ ওয়েটস  এন্ড মেজার্স  অফিসে রাখা প্ল্যাটিনাম ও ইরেডিয়াম সংকর  ধাতুর তৈরি একটি নিরেট চোঙের ভরকে এক কিলোগ্রাম  বলা হয় (It is defined as mass of a cylinder made of  platinum and irridium kept at International Bureau of Weights and Measures in Paris.)
সময়ের একক -সেকেন্ড( Unit of Time(second))--গড় সৌর দিনের 86400 ভাগের এক ভাগকে এক সেকেন্ড বলে ।

সৌরদিন - পৃথিবীর কোনো ভৌগলিক মাধ্যরেখাকে সূর্যের পর পর দুবার অতিক্রম করতে যে সময় লাগে তাকে এক সৌর দিন বলে ।

গড় সৌরদিন - সৌরদিনের মান সারা বছর সমান হয় না ।এক বছরের সমস্ত সৌরদিন যোগ করে 365 দিয়ে ভাগ করে সৌরদিনের যে গড় পাওয়া যায় তাকে গড় সৌর দিন  বলে ।

সেকেন্ডের আধুনিক সংজ্ঞা 

তেজস্ক্রিয় সিজিয়াম -133 পরমাণুর একটি প্রমাণ চুম্বক ক্ষেত্রে 9192631770 সংখ্যক কম্পন সম্পন্ন করতে প্রয়জনীয় সময়কে এক সেকেন্ড বলে ।( I t is the time taken by Cesium atom (133) to complete 9192631770 vibrations in standard magnetic field.)

আয়তনের একক (Units of Volume)-- কোনো বস্তু যে পরিমাণ জায়গা দখল তাকে বস্তুটির আয়তন বলে ।(The amount of space occupied by an object is known its volume).CGS এবং SI পদ্ধতিতে আয়তনের একক যথাক্রমে ঘন সেমি( cm³)এবং ঘন মিটার(m³ )(Its units in CGS and SI system are cm^3 and m^3 respectively.)তরল পদার্থের আয়তনের একক হল লিটার (To measure the volume of liquid Litre(L) unit is used.) 4º C উস্নতায়  এক কিলোগ্রাম জলের আয়তনকে এক লিটার বলে ।(It is the volume of 1 kilogram of water at 4 ^0 C.) এক লিটার  = 1000 c.c (1 L = 1000 cm^3, 1 dm^3 = 1000 cm^3,1 decimeter^3 (1dm^3) = 1000 cm^3 =  1 L.)
  লিটারের সংজ্ঞাতে তাপমাত্রার উল্লেখ (Cause of mentioning 4 degree celsius  in definition of  litre.)-
উস্নতার পরিবর্তনের সঙ্গে সঙ্গে  জলের  আয়তনের পরিবর্তন হয় ।4ºC উস্নতায় জলের আয়তন সর্বনিম্ন হয় ।4ºC থেকে  উস্নতা বাড়লে বা কমলে জলের আয়তনও  বাড়ে ।(Volume of water changes with temperature. But its minimum volume is at 4ºC celsius due to its anomalous expansion.Its volume increases irrespective of increase or decrease of temperature from 4 degree celsius.)

ঘনত্ব (Density) - 
পদার্থের একক আয়তনের ভরকে ঘনত্ব বলে ।যদি একটি বস্তুর ভর M এবং আয়তন V হয় তাহলে ঘনত্ব হবে  M/V CGS এবং SI পদ্ধতিতে এর একক হল যথাক্রমে g/cm³  এবং kg/m³ |(It is the mass of unit volume of matter.If the mass of an object is M and its volume is V then its density is M/V.Its unit in CGS and SI system are g/cm^3 and kg/m^3 respectively.)

1 kg/m³ = 1000 g/10⁶cm³ = 1/1000 g/ cm³or 1 g/cm³ = 1000 kg / m³
বিভিন্ন মাত্রার একক (Units of different sizes) - 
অতি ক্ষুদ্র দৈর্ঘ্য পরিমাপের ক্ষেত্রে নিন্নলিখিত একক গুলি ব্যবহৃত হয় (To measure extremely small length the following units are in use).
1 Micron = 10⁻⁶ m এটি আণুবীক্ষণিক দৈর্ঘ্য মাপের ক্ষেত্রে ব্যবহৃত হয় (used to measure microscopic object).
1 Nanometer(nm) = 10⁻⁹m. ,আলোর তরঙ্গদৈর্ঘ্য পরিমাপে ব্যবহৃত হয় ।(used to measure wave length of light.)
1 Angstrom(A^0) =  10⁻¹ºmআলোর তরঙ্গদৈর্ঘ্য পরিমাপে ব্যবহৃত হয় ।(  used to measure wave length.)

1 X - unit = 10⁻¹³ m,পরমাণুর ব্যাসার্ধ পরিমাপে ব্যবহৃত হয় ( used to measure radius of atom).
1 fermi = = 10⁻¹⁵ m ,পরমাণুর নিউক্লিয়াসের ব্যাসার্ধ পরিমাপে কাজে লাগে (used to measure radius of nucleus.)
অত্যাধিক বৃহৎ দৈর্ঘ্য পরিমাপে নিম্নলিখিত একক গুলি ব্যবহৃত হয় ।(To measure extremely large length following units are used.)
1 Astronomical unit (AU)= 1.4960x10¹¹ m , নক্ষত্রের দূরত্ব পরিমাপে কাজে  লাগে ।(used to measure  distances between stars) .
আলোকবর্ষ - শুন্য মাধ্যমে আলো এক বছরে যে দূরত্ব অতিক্রম করে তাকে এক আলোকবর্ষ বলে ।এক আলোকবর্ষ = 9.46 x 10¹² km,নক্ষত্রের দূরত্ব ও গ্যালাক্সির দৈর্ঘ্য মাপার ক্ষেত্রে ব্যবহৃত হয় ।(1 Light year = Distance traversed by light in vacuum in one year =9.46 x 10¹² km used to measure distances between stars and length of  galaxies.)

ভরের বিভিন্ন একক (Different types of units of mass.)
পারমানবিক ভর একক(u) - 1 u = 1.66054x10⁻²⁷ kg,পরমাণুর ভর পরিমাপে কাজে লাগে ।(1 atomic mass unit (u) = 1.66054x10⁻²⁷ kg ,used to measure atomic mass.)

ক্যারেট - 1 carat = 0.2 g ,সোনা ও হীরা পরিমাপে কাজে লাগে (1 carat = 0.2 g used  in measurement of mass of gold and diamond.)
প্রাকৃতিক রাশির মাত্রা (Dimensions of Physical Quantity) 
কোনো ভৌত রাশির মধ্যে মূল এককগুলি যে ঘাতে অবস্থান করে তাকে ওই রাশির মাত্রা বলে ।(It is a combination of powers of fundamental units( units of mass ,length, time etc) that constitute  a physical quantity.)
মৌলিক  রাশি গুলির মাত্রা নিম্নলিখিত ভাবে প্রকাশ করা হয় ।(Dimension of fundamental units is expressed in the following way).
ভরএর মাত্রা   = M, দৈর্ঘ্য = L, সময় = T,তাপমাত্রা = ፀ,তড়িৎ প্রবাহমাত্র = I ,আলোর তীব্রতা  =J, পদার্থের পরিমান = N (Mass = M,Length = L, Time = T, Temperature = theta ,Electric current = I, Light intensity = J, Amount of matter = N.)

কয়েকটি রাশির মাত্রীয় সংকেত ও একক (Dimensional formula of different quantities and units)

      

রাশি	রাশির পরিচয়	মাত্রীয় সংকেত	মাত্রীয় সমীকরণ	SI একক
1.ক্ষেত্রফল(A)	দৈর্ঘ্য x প্রস্থ	[L²]বা [MºL²Tº]	[ A]=  [MºL²Tº]	m²
2.আয়তন (V)	দৈর্ঘ্য x প্রস্থ x উচ্চতা	L³ = [MºL³Tº]	[ V] = [MºL³Tº]	m³
3.ঘনত্ব( ρ)	ভর / আয়তন	[M/L³] বা[ ML⁻³] বা [ML⁻³Tº]	[ρ] = [ ML⁻³]	kg/m³
4.বেগ (v)	সরণ / সময়	[ LT⁻¹] বা [Mº LT⁻¹]	[v ]=  [Mº LT⁻¹]	ms⁻¹
5.ত্বরণ (a)	বেগের পরিবর্তন /সময়	[LT⁻²] বা [M⁰LT⁻²]	[a ]= [M⁰LT⁻²]	ms⁻²
6.বল (F)	ভর xত্বরণ	[MLT⁻²]	[F] = [MLT⁻²]	N বা  kgms⁻²
7.কাৰ্য্ বা শক্তি(W)	বল x সরণ	[ MLT⁻²] x [L ]= [ML²T⁻²]	[ W] =[ML²T⁻²]	kgm²s⁻²
8.চাপ (P)	বল /ক্ষেত্রফল	[ MLT⁻²]/ [L²] = [ML⁻¹ T⁻² ]	[P ]=  [ML⁻¹ T⁻² ]	Nm⁻²
9.ক্ষমতা(p )	কার্য / সময়	[ML²T⁻²]/ [T ]  =[ML²T⁻³]	[ p ]= [ML²T⁻³]	Js⁻¹
10.ভরবেগ	ভর x বেগ	[M] [LT⁻¹ ] = [MLT⁻¹]		kgms⁻¹

মাত্রার সমগোত্রীয়তা(Principle of Homogeneity of Dimensions)

নীচের সাধারণ সমীকরণটি বিবেচনা করে,

A + B = C, এই সমীকরণটি পদার্থবিদ‍্যার হলে, A,B ও C হল ভৌত রাশি, তিনটি রাশির মাত্রা একই হবে।কারণ মাত্রা এক না হলে সমীকরণটির কোন অর্থ হয় না।যদি A দৈর্ঘ‍্য হয় তাহলে B ও দৈর্ঘ‍্য হবে।C এর ও মাত্রা হবে দৈর্ঘ‍্য।একেই বলে মাত্রার  সমগোত্রীয়তা বলে।

মাত্রীক বিশ্লেষণের প্রয়োগ:

চারটি গুরুত্বপূর্ণ প্রয়োগ আছে -

1.সমীকরণের সত‍্যতা যাচাই করা যায়।

2.যে কোনো ঘটনায় সংযুক্ত ভৌত রাশিরগুলির মধ‍্যে সমপর্ক স্থাপন করা যায়।

3.কোনো সমীকরণের মধ‍্যে অবস্থিত ধ্রুবকের মাএা নির্ণয় করা যায়।

4 এক এককের পদ্ধতি থেকে অন‍্য এককের পদ্ধতিতে&nbsp; রূপান্তর করা যায়।

যে সকল রাশি এককহীন রাশি সেগুলি মাত্রাহীন রাশিও হয় ।আপেক্ষিক গুরুত্ব ,আনবিক ভর ,বিকৃতি ,প্রতিসরাঙ্ক ,বিবর্ধন ,কোণ প্রভৃতি  হল মাত্রাহীন রাশি । কোণ মাত্রাহীন রাশি হলেও এর একক আছে ।কোনের একক রেডিয়ান । 

গাণিতিক প্রশ্ন :

1. E = m c² সমীকরণটির সত্যতা মাত্রার সাহায্যে যাচাই কর ।

সমাধান : LHS : E(শক্তি ) এর মাত্রা = [ML²T⁻²]

RHS : ভরের মাত্রা x c (বেগ ) এর মাত্রার বর্গ  = [M] x [ LT⁻¹]² = [ML²T⁻²]

LHS = RHS , অর্থাৎ  E = m c²  সমীকরণটি মাত্রাগতভাবে সঠিক ।

2. v² = u² + 2aS সমীকরণটির সত্যতা মাত্রার সাহায্যে যাচাই কর ।

সমাধান : 

বাম দিকের  v² এর মাত্রা = বেগের মাত্রার বর্গ = [ LT⁻¹]² =  [L²T⁻²]

ডান দিকের  u² এর মাত্রা = বেগের মাত্রার বর্গ = [ LT⁻¹]² =  [L²T⁻²] , 2aS এর মাত্রা = ত্বরণের মাত্রা x  সরণের মাত্রা =  [LT⁻²] x[ L] = [ LT⁻¹]² = [L²T⁻²]

উভয় দিকের প্রত্যেক অংশের মাত্রা সমান । অতএব সমীকরণটি মাত্রাগত দিক থেকে সঠিক ।

3.F = ma সমীকরণটির সত্যতা মাত্রার সাহায্যে যাচাই করো ।

সমাধান - বামদিকের বল (F) এর মাত্রা =  [MLT⁻²]

ডানদিকের মাত্রা = ভর (m) এর মাত্রা x ত্বরণ (a) এর মাত্রা = [M] x [LT⁻²] = [MLT⁻²]

∴ F = ma সমীকরণটি মাত্রাগতভাবে সঠিক ।

দৈর্ঘ্য পরিমাপ (Measurement of Lenght):

সাধারণ স্কেল :দৈর্ঘ্য পরিমাপের জন্য যে যন্ত্র ব্যবহার করা হয় তাকে সাধারণ স্কেল বলে ।এটি পাতলা কাঠ বা প্লাস্টিকের বা ইস্পাতের তৈরি হয় ।

পরিমাপে ত্রুটি :

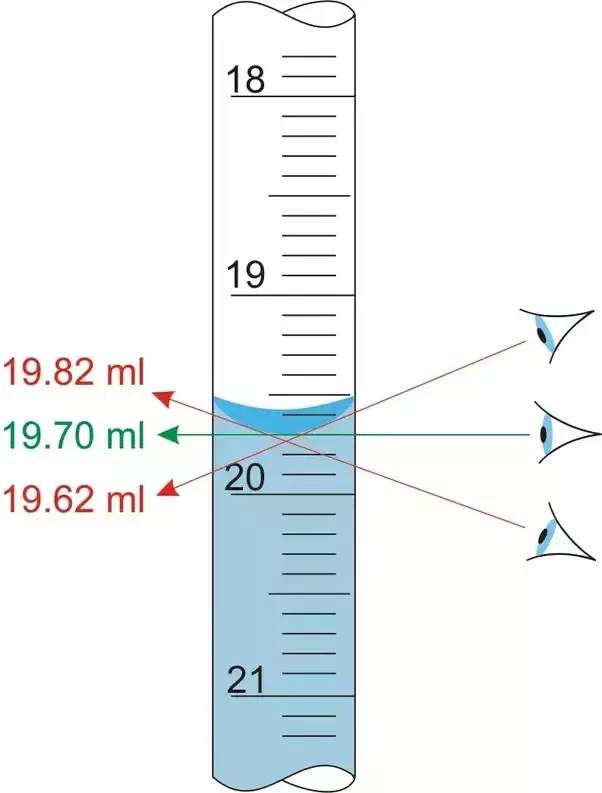
লম্বন ভুল : স্কেল এর সাহায্যে পাঠ নেওয়ার সময় চোখ স্কেল এর পাঠ বিন্দুর সঙ্গে লম্ব ভাবে না থেকে হেলানো অবস্থায় থাকলে পাঠে যে ত্রুটি হয় তাকে লম্বন ত্রুটি  বলে ।

     

সময়ের পরিমাপ (Measurementof Time):

কোনো ঘটনা নিৰ্দিষ্ট সময়ের অবকাশে ঘটলে ওই অবকাশ সময়ের পরিমাপ দেয় ।এটাই সময় পরিমাপের নীতি ।প্রাচীন কালে পৃথিবীর আহ্নিক গতিকে কাজে লাগিয়ে সূর্য ঘড়ির সাহায্যে সময় পরিমাপ করা হতো ।নির্ভুলভাবে সময় পরিমাপের জন্য ক্রোনোমিটার ,সেন্ট্রনাম ,ইলেকট্রনিক ডিজিটাল ঘড়ি  ও সিজিয়াম ঘড়ি ব্যবহৃত হয় ।

স্টপওয়াচ - এই ধরনের ঘড়িকে ইচ্ছামত চালানো ও বন্ধ করা যায় ,এই ঘড়িকে স্টপওয়াচ বা বিরাম ঘড়ি বলে ।বিভিন্ন প্রতিযোগিতায় এই ঘড়ির সাহায্যে সময় মাপা হয় ।এর সাহায্যে 1/10 সেকেন্ড পর্যন্ত নির্ভুল সময় মাপা যায় ।

 

মেট্ৰোনাম - এই ঘড়ির সাহায্যে উপগ্রহ উৎক্ষেপণের সময় নির্ভুলভাবে সময় পরিমাপ করা হয় ।

ক্রোনোমিটার - এই ঘড়ির সাহায্যে গ্রীনিচের সময় সঠিকভাবে পরিমাপ করা হয় ।

সিজিয়াম ঘড়ি - চৌম্বক ক্ষেত্রে ¹³³Cs পরমাণুর যে কম্পন হয় তাকে কাজে লাগিয়ে এই ঘড়ি তৈরি করা হয় ।এই ঘড়িতে 6000 বছর সময়ে 1 সেকেন্ড ত্রুটি দেখা যায় ।এই ত্রুটি অত্যন্ত নগন্য ।

ইলেকট্রনিক ডিজিটাল ঘড়ি - কোয়ার্টজ কেলাসের কম্পনকেইলেকট্রনিক বর্তনীর সাহায্যে  কাজে লাগিয়ে এই ঘড়ি তৈরি করা হয় ।এই ঘড়ির সাহায্যে এক মাইক্রো সেকেন্ড (10⁻⁶) পর্যন্ত নির্ভুলভাবে পরিমাপ করা যায় ।

ভরের পরিমাপ (Measurement of Mass):

সাধারণ তুলাযন্ত্র (Common Balance) - এই যন্ত্রের সাহায্যে আমরা ভর পরিমাপ করি ।

https://photos.app.goo.gl/RgXDiVNveUECdA9o8

এটি মূলত একটি প্রথম শ্রেণীর লিভার যার বল বহু  = রোধবহু ।ভর নির্ণয়ের জন্য তুলযন্ত্রের বাম দিকের পাল্লায় বস্তু রেখে ও ডানদিকের পাল্লায় প্রমান মানের বাটখারা রেখে তুলাদণ্ডটি অনুভূমিক করা হয় ।তুলাদন্ডটি অনুভূমিক থাকলে ভ্রামকের নীতি অনুসারে লেখা যায় -

বস্তুর ওজন  X  OA   = বাটখারার ওজন X OB

বস্তুর ভর х g x OA = বাটখারার ভর x g х OB

বস্তুর ভর = বাটখারার ভর ( ∵ OA = OB)

এই নীতির উপর ভিত্তি করে তুলাযন্ত্র কাজ করে ।

ওজন বাস্কের বাট্খারাগুলির ভরের অনুপাত 5:2:2:1 রাখার কারণ -

বাট্খারাগুলি এই অনুপাতে থাকলে সবচেয়ে কম সংখ্যক বাটখারা ব্যবহার করে 1 থেকে 10 গ্রাম বা 10 গ্রাম থেকে 100 গ্রাম বা 10 মিলিগ্রাম থেকে 100 মিলিগ্রাম বা 100 মিলিগ্রাম থেকে 1000 মিলিগ্রাম ভর সহজে পরিমাপ করা যায় ।যেমন 49.32 গ্রাম ভর মাপতে হলে যে বাট্খারাগুলি ব্যবহার করতে হবে তা হল 20 g +20 g +5 g +2 g +2 g+ 200 mg + 100 mg +20 mg |

( 10 মিলিগ্রামের কম ভর মাপের ক্ষেত্রে রাইডারের ব্যবস্থা থাকে )

ভালো তুলাযন্ত্রের আবশ্যকীয় গুণাবলী :

1.সুবেদী তুলা - যে তুলা যন্ত্রে ভরের সামান্য পার্থক্য বোঝা যায় তাকে সুবেদী তুলা বলে । তুলাযন্ত্রটি সুবেদী হওয়া প্রয়োজন ।তুলাযন্ত্র সুবেদী হওয়ার শর্ত গুলি হল - a ).তুলাদণ্ডটি র দুই বাহূ দীর্ঘ ও হালকা হওয়া দরকার । b).তুলাপাত্রদুটি হালকা হওয়া প্রয়োজন । c)সূচকটি লম্বা হওয়া দরকার ।

2.তুলা সুস্থিত হওয়া প্রয়োজন -তুলাযন্ত্রের সূচকের দোলন যেন খুব বেশি দীর্ঘস্থায়ী না হয় ।

3.তুলা নির্ভুল হওয়া প্রয়োজন - তুলাপাত্রদুটি খালি থাকলে যেন তুলাদন্ডটি অনুভূমিক থাকে ।

নির্ভুল হওয়ার শর্ত - a) তুলাদণ্ডের দুই বাহুর দৈর্ঘ্য ও ভর যেন সমান হয় । b) তুলাপাত্র দুটির ভর সমান হওয়া দরকার ।c) অনুভূমিক অবস্থায় তুলাদণ্ডের ভারকেন্দ্র যেন আলম্বের নীচে অবস্থান করে ।

d) তুলা দৃঢ় হওয়া প্রয়োজন অর্থাৎ ভর চাপালে তুলাদণ্ড যেন বেঁকে না যায় ।

4.তুলাযন্ত্রটি যেন দৃঢ় হয় -তুলাযন্ত্রের বিভিন্ন অংশ যেন মজবুত হয় ।

অসম ভরের তুলাপাত্র যুক্ত তুলাযন্ত্রে ভর নির্ণয় -

তুলাপাত্রদুটির ভর অসমান হলে ভর পরিমাপে ত্রুটি হয় । এক্ষেত্রে বস্তুটিকে একবার বামপাত্রে এবং একবার ডানপাত্রে রেখে ভর নির্ণয় করতে হবে ।দুই ক্ষেত্রে ভর m₁ ও m₂ হলে বস্তুটির প্রকৃত ভর হবে m = (m₁ + m₂)/2 |

অসম দৈর্ঘ্যর বাহুযুক্ত তুলাযন্ত্রের সাহায্যে বস্তুর ভর নির্ণয় - 

দুলাদণ্ডের দুই বাহুর দৈর্ঘ্য অসমান হলে ভর নির্ণয়ে ত্রুটি দেখা যায় ।এক্ষেত্রে প্রথমে বামপত্রে বস্তু রেখে পরে ডানপাত্রে রেখে ভর নির্ণয় করা হয় । এই দুই ক্ষেত্রে ভর যথাক্রমে m₁ এবং m₂ হলে প্রকৃত ভর m হলে m = √(m₁m₂) |

আয়তন মাপক চোঙ এবং সাধারণ তুলার সাহায্যে অসম আকৃতির বস্তুর আয়তন ও উহার উপাদানের ঘনত্ব নির্ণয় 

       

প্রথমে সাধারণ তুলার সাহায্যে বস্তুর ভর নির্ণয় করা হল ।মনে করি বস্তুটির ভর = M |মাপক চোঙে কিছুটা জল নিয়ে তার পাঠ নেওয়া হলো ।মনেকরি এই পাঠ V₁ cm³ | এরপর অসম আকৃতির বস্তুটিকে ধীরে ধীরে জলের মধ্যে ডুবিয়ে আবার মাপনী চোঙের জলের আয়তনের পাঠ নেওয়া হল ।মনেকরি এই পাঠ V₂ cm³ | বস্তুটির আয়তন হবে (V₂ -  V₁) cm³ |

অতএব বস্তুটির ঘনত্ব =  বস্তুর ভর /বস্তুর আয়তন  = M/(V₂ -  V₁) g/cm³ 

গানিতিক উদাহরনঃ1. একটি লোহার  ভর 380 g এবং আয়তন 50 cm³ হলে, লোহার ঘনত্ব কত হবে ?

সমাধান - 

আমরা জানি  ঘনত্ব  = ভর /আয়তন  = 380/50 g cm⁻³ = 7.6  g cm⁻³

2.CGS পদ্ধতিতে সোনার ঘনত্ব 19.3 গ্রাম /সেমি³ হলে SI এককে সোনার ঘনত্ব কত ?

সমাধান : 

সোনার ঘনত্ব = 19.3 গ্রাম /সেমি³ ( 1 গ্রাম = 1/1000 kg = 0.001 kg | (1 cm)³ = (1/100 m)³ = (0.01m)³ = 0.000001 m³ )

∴ সোনার ঘনত্ব=  19.3 গ্রাম /সেমি³ = 19.3 x 0.001 /0.000001 kg/m³ = 19300 kg/m³ |

3. 4⁰C তাপমাত্রায় 20 g জলে একটি পাত্র পুরোপুরি ভর্তি হয়, ওই পাত্রে 16 g কেরোসিন ধরলে কেরোসিনের ঘনত্ব কত ?

সমাধান :

4⁰C তাপমাত্রায় 1 গ্রাম জলের আয়তন 1 cm³ | অতএব জলের আয়তন 20  cm³  অর্থাৎ পাত্রটির আয়তন 20  cm³  ।

∴ 16 গ্রাম কেরোসিনের আয়তন 20  cm³ ।

সুতরাং কেরোসিনের ঘনত্ব = 16/20 g cm⁻³ = 0.8 g cm⁻³ |

                                           

অতিসংক্ষিপ্ত উত্তরভিত্তিক প্রশ্ন -

১.তড়িৎ প্রবাহমাত্রা কী রাশি ?

২.SI পদ্ধতিতে ক্ষেত্রফলের একক কী ?

৩.বস্তুর ভার কোন যন্ত্রের সাহায্যে মাপা হয় ?

৪.ঘন কোনের একক কী ?

৫.উস্নতা ,কার্য্য ,ভর ,বল ও ক্ষেত্রফলের মধ্যে কোনগুলি স্কেলার রাশি আর কোনগুলি ভেক্টর রাশি ?

৬.ঘনত্বের SI ও CGS এককের মধ্যে সম্পর্ক লেখো ।

৭.একটি একক বিহীন রাশির উদাহরণ দাও ।

৮.মাত্রা নেই কিন্তু একক আছে এরূপ একটি রাশির উদাহরণ দাও ।

৯.সাধারণ তুলাযন্ত্রের বাট্খারাগুলির ভরের অনুপাত কত ?

    

স্তম্ভ মেলাও    

বামস্তম্ভ	ডানস্তম্ভ
i)ত্বরণ	a)) [MLT⁻²]
ii) ওজন	b)[LT⁻²]
iii)ভরবেগ	c)[ MLT⁻¹]
iv) শক্তি	d)ML²T⁻²][

          

   স্তম্ভ মেলাও                                          

বামস্তম্ভ	ডানস্তম্ভ
i) 10⁻⁶  মিটার	a ) ফার্মি
ii) 10⁻¹³ মিটার	b) আনস্ট্রম
iii) 10⁻¹⁰ মিটার	c) মাইক্রন
iv) 10⁻¹⁵মিটার	d) X- একক

          

সঠিক উত্তরটি নির্বাচন কর (MCQ): https://forms.gle/mkBnDon4uJFvPf9M7

1.দৈর্ঘ্য পরিমাপের সবচেয়ে বড় একক  হল  - 

A) আলোকবর্ষ   B) মিটার   C) কিলোমিটার  D) পারসেক 

2.1 nm = কত মিটার ?

A) 100 B) 1000 C) 10⁻⁹ D) 10

3.SI পদ্ধতিতে উষ্নতার এককহল - 

A ) K  B) ⁰K C) ⁰F D) ⁰C

4. তিনটি মৌলিক একক দ্বারা গঠিত একটি স্কেলার ও একটি ভেক্টর রাশি হল -

A) দ্রুতি ,বেগ  Bএর ) সরণ , কার্য  C) কার্য  , বল  D) ক্ষমতা , ত্বরণ 

5.সাধারণ তুলাযন্ত্রের ওজন বাক্সের বাট্খারাগুলির ওজন কোন অনুপাতে থাকে ?

A) 1: 2:3: 5 B) 1:2:2:5 C) 1:2:2:3  D) 1:2:3:4

6. মাত্রাহীন কিন্তূ একক যুক্ত একটি রাশি হল -

    A) চাপ  B) বেগ  C) ঘনকোন D) ক্ষেত্রফল 

7.1 ⁰A  = কত মিটার ?

A) 10⁻⁶ B) 10⁻⁸ C) 10⁻¹⁵ D) 10⁻¹⁰

8.নিম্নলিখিত একক গুলির মধ্যে কোনটি মৌলিক একক ?

A) আলোকবর্ষ  B) নিউটন  C) লিটার D) মিটার সে ⁻²

9.কোন রাশির মাত্রা হল [ MLT⁻²]

A) ঘনত্ব  B) বেগ  C) কার্য  D) বল 

10.ত্বরণের মাত্রা  হল -

A) LT⁻² B) LT²  C) LT  D) LT⁻¹

11.নীচের রাশিগুলির মধ্যে এককহীন রাশিটি হল - 

A) আপেক্ষিক গুরুত্ত্ব  B ) বেগ  C) ভরবেগ D) ত্বরণ 

12. 4⁰C উষ্নতায়  5 cm³ জলের ভর হল 

A) 5 g  B) 3 g  C) 4 g D) 20 g

13,কার্যের মাত্রা হল 

A) ML²T⁻²  B) MLT⁻² C) MLT⁻¹  D) ML²T²

14.সাধারণ তুলা দিয়ে মাপা হয়  বস্তুর 

A) ওজন  B) আয়তন   C) ভর  D) ভরবেগ 

15. SI পদ্ধতিতে ক্ষেত্রফলের একক -

A) সেমি²  B) মি² C) সেমি D) মিটার