গড় দ্রুতি = মোট অতিক্রান্ত দূরত্ব /মোট গৃহীত সময়
তাৎক্ষণিক দ্রুতি = dx/dt
গড় দ্রুতি ঃ
i) যখন অর্ধ সময় V₁ দ্রুতিতে এবং বাকি অর্ধেক সময় V₂ দ্রুতিতে চলে তখন গড় দ্রুতি হবে -
Vₐ = ( V₁ + V₂)/2
ii) যখন অর্ধেক দূরত্ব V₁ দ্রুতিতে এবং বাকি অর্ধেক দূরত্ব V₁ দ্রুতিতে চলে তখন গড় দ্রুতি হবে
Vₐ = 2 V₁V₂/ (V₁ + V₂)
iii) যখন x₁ দূরত্ব V₁ দ্রুতিতে এবং x₂ দূরত্ব V₂ দ্রুতিতে অতিক্রম করে তখণ দ্রুতি হয় -
Vₐ = ( x₁ + x₂)/ ( x₁/V₁ + x₂ /V₂ )
iv) যখন V₁ দ্রুতিতে t₁ সময় এবং V₂ দ্রুতিতে t₂ সময় চলে তখন গড় দ্রুতি হয়
Vₐ = (V₁ t₁ + V₂ t₂)/(t₁ + t₂)
o কোনো চলমান বস্তুর ক্ষেত্রে দূরত্ব কখনো শূন্য বা ঋণাত্মক হয় না , সময়ের সঙ্গে সর্বদা বৃদ্ধি পায় ।
o সময়ের সঙ্গে দূরত্ব হ্রাস পায় না ।
o দূরত্ব সরণের থেকে কম হতে পারে না ।
o যখন দূরত্ব সরণের মানের সঙ্গে সমান হয় তখন বস্তুকণাটি সরলরেখায় গতিশীল হয় এবং পথের কোনো অংশই বস্তুকণাটি দ্বিতীয়বার অতিক্রম করে না ।
o সম বেগে গতিশীল কণার ক্ষেত্রে দ্রুতি এবং গতির অভিমুখ অপরিবর্তিত থাকে ।
o সমবেগে গতিশীল কণা সম দ্রুতিতে থাকে , কিন্তু সমদ্রুতি সম্পন্ন বস্তুকণা সমবেগে নাও থাকতে পারে ।
o দ্রুতি বাড়লে ত্বরণ দেখা যায় ।
o যখন দ্রুতি হ্ৰাস পায় তখন মন্দন উৎপন্ন হয় ।
ঋণাত্মক ত্বরণকে কিন্তু মন্দন বলে না ।
যখন কোনো বস্তুকণার প্রাথমিক বেগ [- 2 i ]ms⁻¹ এবং ত্বরণ [ - 3i ] ms⁻² হয় তখন বস্তুটি ত্বরানিত্ব হয় ।
প্রকৃতপক্ষে যখন বেগ ও ত্বরণ এর দিক একই হয় তখন দ্রুতি বৃদ্ধি পায় এবং ত্বরণ দেখা দেয় । যখন বেগ ও ত্বরণের দিক বিপরীত হয় তখন দ্রুতি হ্রাস পায় এবং মন্দন দেখা যায় ।
যখন গতিবেগ এবং ত্বরণ পরস্পর লম্বভাবে ক্রিয়া করে তখন দ্রুতি পরিবর্তিত হয় না ।
о x - t লেখচিত্রের নতিই হল তাৎক্ষণিক বেগ ।
о v - t লেখচিত্রের নতিই হল তাৎক্ষণিক ত্বরণ ।
о ∫ Vdt হল সরণের পরিমাপ ।
о x
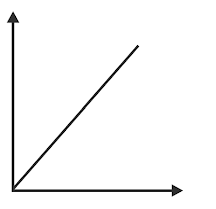t
x
tক্রমবর্ধমান গতিবেগ
x
t ক্রমহ্রাসমান গতিবেগ
s-t লেখচিত্রে কোনো বিন্দুতে অঙ্কিত স্পর্শকের নতিই হলো ওই বিন্দুতে তাৎক্ষণিক গতিবেগ ।
∆t সময়ে গতিবেগের পরিবর্তণ ∆S হলে গড় গতিবেগ হবে ∆S /∆t
সম ত্বরণ ( Uniform Acceleration) :
এক্ষেত্রে গতিবেগ -সময় লেখচিত্র সরলরেখা হয় ।
ক্রমহ্রাসমান ত্বরণ (decreasing acceleration):
এক্ষেত্রে ত্বরণ সময়ের সঙ্গে সঙ্গে হ্রাস পায় ।উপরের লেখাচিত্রের নতি ক্রমশ সময়ের সঙ্গে হ্ৰাস পেয়েছে ।
ক্রমবর্ধমান ত্বরণ ( Increasing Acceleration):
এক্ষেত্রে ত্বরণ সময়ের সঙ্গে সঙ্গে বৃদ্ধি পায় ।উপরের লেখাচিত্রে নতি ক্রমশ বৃদ্ধি পেয়েছে ।
⃝ সুসম ত্বরণের ক্ষেত্রে :
v = u + at
s = ut + 1/2 at² = 1/2( u+ v) t = vt - 1/2 at²
v² = u² + 2 as
[ u= প্রাথমিক বেগ , v = অন্তিম বেগ , a = সুষম ত্বরণ , s = অতিক্রান্ত দূরত্ব , t = সময় ]
🌑 v = 2 + 3t সমীকরণের জন্য
i) প্রাথমিক গতিবেগ = 2 ms⁻¹
ii) সুষম ত্বরণ = 3 ms⁻²
🌑 s = 10t + 5t² সমীকরণের জন্য
i) প্রাথমিক বেগ = 10 ms⁻¹
ii) সুষম ত্বরণ = 10 ms⁻²
v
tউপরের লেখচিত্রটি কী সম্ভব ?
নিশ্চিত ভাবেই নয় , কারণ একই সময়ে দুটি গতিবেগ থাকতে পারে না ।
x
tনিজে করো ।
🌑 অসম ত্বরণের একটি সমীকরণ :
x :at + bt² + ct³
dx/dt = a + 2bt + 3ct² ⇒ তাৎক্ষণিক গতিবেগ ।
d²x/dt² = 2b + 6ct ⇒ তাৎক্ষণিক ত্বরণ ।
🌑 একটি বস্তু কণার গতিবেগ শুন্য হলেও ত্বরণ থাকতে পারে ।
যখন একটি বস্তুকে সোজা উপরের দিকে ছোড়া হয় তখন সর্বোচ্চ বিন্দুতে গতিবেগ শূন্য কিন্তু ত্বরণ g নিম্নাভিমুখে কাজ করে ।
দোলকের গতির প্রান্তীয় অবস্থানে গতিবেগ শূন্য হয় কিন্তু ত্বরণ শূন্য নয় ।
উপরের লেখচিত্রে ছায়াযুক্ত অঞ্চলটি হল সরণের পরিমাপ । এটিকে নীচের সমীকরণের আকারে লেখা যায় -
∫v dt
Q1 . ঊর্ধ্বমুখী 15 m/s বেগে ধাবমান একটি বেলুন থেকে 50 m উচ্চতা থেকে একটি পাথর ফেলা হলো । পাথরটি কত সময় পরে মাটিতে পড়বে ? ( g = 10 m/s)
A) 5 s B) 7 s
C) 9 s D) 3 s
Q2. একটি গাড়ি স্থিরাবস্থা থেকে প্রথমে 6 m/s² ত্বরণে এবং পরে 3 m/s² মন্দনে চলে 12 s এ পুনরায় স্থীর অবস্থায় আসে । নীচের কোনটি সত্য ?
A) গাড়িটির সর্বোচ্চ বেগ 36 m/s
B) মোট অতিক্রান্ত দূরত্ব 144 m
C) গড় গতিবেগ হলো 24 m/s
D) গাড়িটি 9 s ধরে ত্বরান্বিত হয় ।
Q3.একটি বস্তু স্থির ক্ষমতায় সরলরেখায় চলছে । t সময়ে অতিক্রান্ত দূরত্ব নীচের কোনটির সঙ্গে সমানুপাতিক ?
A) t³⁄² B) t¹⁄⁴ C) t² D) t¹∕²
Q4.স্থীর ত্বরণে গতিশীল একটি ট্রেনের চালক ও গার্ড একটি খুঁটিকে যথাক্রমে u এবং v গতিবেগে অতিক্রম করে । ট্রেনের মধ্য বিন্দু কত গতিবেগে খুটিটিকে অতিক্রম করে ?
A) √[(u + v)/2] B) √(uv) C) √(u² + v²) D) √[(u² + v²)/2]
Q5. 
একটি রড AB উলম্ব ও অনুভূমিক পিছেলে পড়ছে । রডটি যখন অনুভূমিকের সঙ্গে Ө কোণ করে তখন B প্রান্তের বেগ V₀ হলে A প্রান্তের গতিবেগ কত হবে ?
A) V₀ cosӨ B) V₀ cotӨ
C) V₀ tanӨ D) V₀ sinӨ
Q6.একটি গাড়ী সরল পথে চলছে । গাড়িটি অর্ধেক রাস্তা V₁ গতিবেগে এবং বাকি অর্ধেক রাস্তা V₂ বেগে গমন করে । গাড়িটির গড় গতিবেগ হবে -
A) √( V₁V₂) B) (V₁ + V₂)/2
C) 2V₁V₂/(V₁+V₂) D) √( V₁²+V₂²)/2
Q7. একটি গাড়ি সরল পথে চলছে । মোট সময়ের প্রথম অর্ধেক V₁ বেগে এবং দ্বিতীয় অর্ধেক সময় V₂ বেগে চলে , গাড়িটির গড় গতিবেগ হবে -
A) √( V₁V₂) B) (V₁ + V₂)/2
Q8. সরণ(s) ও সময় (t ) s = 1 + 2t + 3t² - t³ এই সমীকরণ অনুযায়ী সম্পর্কিত হলে নীচের কোনটি সঠিক ?
A) প্রাথমিক সরণ শূন্য
B) প্রাথমিক গতিবেগ 1 m s⁻¹
C) প্রাথমিক ত্বরণ 16 m s⁻²
D) t = 1 s এ ত্বরণ শূন্য হবে ।
Q9.একটি বল অভিকর্ষের অধীনে অবাধে পতনশীল । 0 -3 s এ অতিক্রান্ত দূরত্ব এবং 4 s থেকে 5s এ অতিক্রান্ত দূরত্বের অনুপাত -
A) 1 :1 B) 1: 16 C) 9:16 D) 16 :25
Q10.একটি ছাত্র একটি স্থির বাস থেকে 50 m দূরে আছে । বাসটি যখন 1m/s² ত্বরণে চলতে শুরু করে তখন ছাত্রটি V ms⁻¹ বেগে ছুটতে আরম্ভ করে । ছাত্রটি বাসটিকে সবে মাত্র ধরতে পারবে যদি -
A) V = 5 B) V = 8 C) V = 10 D) V = 12
Q11. d উচ্চতা থেকে একটি বলকে ছেড়ে দেওয়া হল । বলটি মাটিতে আঘাত করার পর উলম্ব উচ্চতা d/2 আরোহণ করে । বলটির গতিবেগ v উচ্চতা h এর সঙ্গে নীচের কোণ লেখচিত্র পৰিৱৰ্তিত হয় ।
Q12 একটি বস্তুকণার অবস্থান ভেক্টর r = 4t² i + 3t²j + 2k হলে ত্বরণ হবে -
A) 5 m s⁻² B) 10 m s⁻²
C) 8 m s⁻² D) 0
Q13 . একটি বস্তু স্থিরাবস্থা থেকে যাত্রা করে অভিকর্ষের অধীনে অবাধে পতনশীল । মোট উচ্চতার অর্ধেক শেষ সেকেন্ডে অতিক্রম করে । বস্তুটি মোট উচ্চতাটি অবতরণ করে
A) (2 + √2 ) s B) (√2 +1) s
C) (2 -√2 ) s D) (√2 - 1) s
Q14.একটি গাড়ি P থেকে Q তে 36 km h⁻¹ সুষম দ্রুতিতে গমণ করে এবং ফিরে আসে 45 km h⁻¹ সুষম দ্রুতিতে । যাতায়াতে গড় দ্রুতি কত ?
A) 40.5 km h⁻¹ B) 40 km h⁻¹
C) 0 D) কোনোটিই নয়
Q15. ( 0,0) বিন্দুতে অবস্থিত একটি চোর (l ,0) অবস্থানে একটি পুলিশ কে দেখতে পেলো এবং u সমবেগে y - অক্ষ বরাবর দৌঁড়েতে শুরু করলো । একই সঙ্গে পুলিশও চোরটিকে লক্ষ্য করে v দ্রুতিতে দৌঁড়োতে শুরু করলো । পুলিশ চোরটিকে কত সময়ে ধরতে পারবে ?
A) ul /( v² + u²) B) ul /( v² - u²)
C) vl /( v² + u²) D) vl /( v² - u²)
Q16. V₁ দ্রুতিতে গতিশীল একটি ট্রেনের চালক d দূরত্বে একই লাইনে একই দিকে V₂ দ্রুতিতে গতিশীল অপর একটি ট্রেন দেখতে পেলো । চালক ব্রেক কষে a মন্দন সৃষ্টি করলো । যদি সংঘাত এড়ানো সম্ভব হয় তাহলে -
A) a < (V₁² + V₂²)/2d B) a ＞ (V₁² - V₂²)/d
C)a < (V₁ - V₂)²/2d D) a > (V₁ - V₂)²/2d
Q17.অভিকর্ষের টানে একটি বস্তু 220 m উপর থেকে পড়ছে । সময়ের 0- 2 s ,2 -4 s এবং 4 -6 s অন্তরে অতিক্রান্ত দূরত্বের অনুপাত হলো -A) 1:4:9 B) 1:2:4
C) 1:3:5 D) 1:2:3
Q18. . একটি বস্তুকণা x - অক্ষ বরাবর গতিশীল । t সেকেন্ড সময়ে অতিক্রান্ত সরণ ( মিটারে ) সমীকরণ x = 40 + 12 t - t³ দ্বারা নিয়ন্ত্রিত হয় । স্থির অবস্থায় আসা পর্যন্ত বস্তুকণাটি কত দূরত্ব অতিক্রম করবে ?
A) 16 m B)21m
C) 40 m D) 56 m
Q 19. একটি বস্তু কণা t = 0 সময়ে x = 0 তে অবস্থিত এবং বস্তুকণাটি x অক্ষ বরাবর যাত্রা শুরু করে v = a ✓x গতিবেগ নিয়ে । সময়ের সঙ্গে কণাটির সরণ নীচের কোনটি অনুসারে পরিবর্তিত হয় ?
A) t B) ✓t
C) t² D) কোনোটিই নয়
Q 20. একটি গাড়ি স্থিরাবস্থা থেকে সম ত্বরণে যাত্রা শুরু করে । n তম সেকেন্ডে ও n সেকেন্ডে অতিক্রান্ত দূরত্বের অনুপাত
A) ( 2n - 1)/2n² B) n²/ (2n - 1)
C) ( 2n - 1)/n² D) 1/n²
Q21. একটি বলকে সোজা উপরের দিকে ছোঁড়া হল। বলটি উপরে উঠল এবং শেষে ভূমিতে ফিরে এল। বলটির এই গতির সময় -
a ) বলটির কোন ত্বরণ ছিল না।
b ) বলটির ত্বরণের মান অপরিবর্তিত ছিল ও দিক সর্বদাই সোজা নিচের দিকে ছিল।
c) বলটির ত্বরণের দিক, ওঠা ও নামার সময় আলাদা আলাদা ছিল।
d ) বলটির ত্বরণ সর্বচ্চো বিন্দুতে শূন্য ছিল।
সমাধান :
Q 1 . h = ut + 1/2 g t² থেকে পাই ,
50 = -15 t +1/2 x 10 t²
⇒50 = -15 t + 5 t²
বা t² - 3 t -10 =0
বা ( t - 5) ( t + 2 ) = 0
অতএব t = 5 ( t এর ঋনাত্বক মান গ্রাহ্য নয় )
উত্তর A)
Q2. ধরি গাড়িটি সমত্বরণে t₁ সময় ও সম মন্দনে t₂ সময় চলে ।
অতএব t₁ + t₂ = 12
সর্বোচ্চ বেগ v₀ = 6 t₁ = 3 t₂
⇒2 t₁ = t₂
⇒t₁ = 4 , t₂ = 8 , v₀ = 6 x 4 = 24
অতএব s =গড়বেগ x মোট সময় = 1/2 v₀ ( t₁ + t₂) = 1/2 x 24 x 12 = 144
গড় দ্রুতি = 144/12 = 12
উত্তর - B )
Q3. ক্ষমতা P = F x V ( F = প্রযুক্ত বল , V = বেগ )
= m dv/dt v
⇒ v dv = P/m dt
⇒ ∫ vdv = ∫ P/m dt
বা , v²/2 = P/m t
বা , v = √(2P/m t)
বা dx/dt = √(2P/m t)
⇒ ∫ dx = ∫ √(2P/m t)
⇒ x = √(2P/m ) t³/²
অতএব x ∝ t³/²
উত্তরঃ A)
Q4 . মনে করি ট্রেনের মধ্যবিন্দু খুটিটিকে v₁ বেগে অতিক্রম করে ।
v² = u² + 2a s সমীকরণ থেকে পাই
v₁² = u² + 2a s/2 = u² + 1/2( 2as) = u² + 1/2 ( v² - u² )
= 1/2 ( u² + v²)
উত্তরঃ D)
Q5. AB রড বরাবর B প্রান্তের গতিবেগ V₀ cosθ
A প্রান্তের গতিবেগ Vₐ এর AB বরাবর উপাংশ Vₐ cos ( 90⁰ - θ )
⇒ V₀ cosθ = Vₐ cos ( 90⁰ - θ )
বা V₀ cosθ = Vₐ sin θ
অতএব Vₐ = V₀ cot θ
উত্তরঃ B)
Q6. মনেকরি মোট অতিক্রান্ত দূরত্ব x |
প্রথম অর্ধেক দূরত্ব যেতে সময় = 1/2 x/v₁ ,
দ্বিতীয় অর্ধেক দূরত্ব যেতে সময় = 1/2 x/v₂
মোট সময় = x/2 ( 1/v₁ + 1/v₂ )
অতএব গড় গতিবেগ = মোট অতিক্রান্ত দূরত্ব / মোট সময়
= x /[x/2 ( 1/v₁ + 1/v₂ )]
= 2 v₁ v₂/ (v₁ + v₂ )
উত্তরঃ C )
Q7. ধরি প্রথম অংশ t সময় ও দ্বিতীয় অংশ ও t সময় ধরে চলে ।
মোট অতিক্রান্ত দূরত্ব V₁ t + V₂ t
অতএব গড় গতিবেগ = মোট দূরত্ব / মোট সময়
= (V₁ t + V₂ t )/( t + t )
= (V₁ + V₂ )/2
উত্তরঃ B)
Q8. S = 1 + 2t + 3t² - t³
প্রাথমিক সরণ S₀ = 1 ( t = 0 বসিয়ে )
গতিবেগ V =dS/dt = 2 + 6t -3 t²
⇒প্রাথমিক বেগ = 2 ( t = 0 বসিয়ে )
ত্বরণ dV/dt= 6 - 6t
প্রাথমিক ত্বরণ = 6 ( t = 0 বসিয়ে )
t = 1 হলে ত্বরণ = 6 -6 = 0
উত্তরঃ D)
Q9.তিন সেকেন্ডে অতিক্রান্ত দূরত্ব h₃ = ut + 1/2 gt
= 0 + 1/2 g x3³ = 9/2 g
অনুরূপে 5 সেকেন্ডে অতিক্রান্ত দূরত্ব h₅ = 1/2 g x 5²
এবং 4 সেকেন্ডে অতিক্রান্ত দূরত্ব h₄ = 1/2 x g x 4²
অতএব পঞ্চম সেকেন্ডে অতিক্রান্ত দূরত্ব h₅ - h₄ = 1/2 g x 5² - 1/2 x g x 4²
= 1/2 g x ( 25 - 16 )
= 1/2 g x 9 =9/2 g
নির্ণেয় অনুপাতে = h₃ /(h₅ - h₄) = (9/2g)/ (9/2 g ) = 1
উত্তরঃ A)
Q10 . t সময় পরে বাসটির দূরত্ব হবে 1/2 at² + d = 1/2 x 1 x t² + 50
= 1/2 t² + 50
ছাত্রটি t সময়ে দূরত্ব যায় vt
প্রশ্নানুসারে 1/2 t² + 50 = vt
1/2 t² - vt + 50 = 0
t এর বাস্তব মানের জন্য v² - 4 x1/2 x 50 ⩾ 0
⇒ v² ⩾ 100
অতএব v ⩾ 10
উত্তরঃ C)
Q11.
উত্তরঃ A)
Q12. সরণ , r = 4 t² i + 3 t² j + 2 k
গতিবেগ v = dr/dt = 8t i + 6t j
ত্বরণ d²r/dt² = 8 i + 6 j
|d²r/dt² | = √ ( 8² + 6² ) = 10
উত্তর - B)
Q13.ধরি মোট উচ্চতা h ।
প্রশ্নানুসারে,
h = 1/2 g t²
এবং h/2 = 1/2 g ( t -1)²
উপরের দুই সমীকরণ ভাগ করে পাই ,
2 = ( t /t-1)²
⇒ t/t-1 = √ 2
⇒ t = √ 2 /( √ 2 -1) = √ 2 ( √ 2 + 1) = 2 + √ 2
উত্তরঃ A)
Q14. ধরি স্থানদুটির মধ্য দূরত্ব x
অতএব মোট অতিক্রান্ত দূরত্ব = 2 x
গড় দ্রুতি = মোট দূরত্ব / মোট সময়
= 2x / ( x/36 + x/45)
= 2 x 36x45 / ( 36 + 45)
= 40 km/hr
উত্তরঃ B)
Q15.
তাৎক্ষণিক আপেক্ষিক বেগ = v - u cos α
ধরি t সময়ে পুলিশ চোর ধরতে পারবে
অতএব
(v - u cos α ) t = lআবার v cos α t = u t
উপরের দুই সমীকরণ থেকে পাই ,
(v - u u/v ) t = l
⇒ ( v² - u²) /v t =l
⇒ t = vl/ (v² - u²)
অতএব , উত্তরঃ D)
Q16. ধরি t সময়ে ট্রেন দুটি স্পর্শকরে পিছনের ট্রেন থেমে যাবে ,
t সময়ে সামনের ট্রেন যাবে v₂ t
পিছনের ট্রেনটি যাবে v₁ t - 1/2 a t²
প্রশ্নানুসারে, v₂ t + d = v₁ t - 1/2 a t²
⇒ 1/2 a t² - ( v₁ - v₂ ) t + d = 0
উপরের সমীকরণের কোনো বাস্তব বীজ থাকবে না যদি ,
( v₁ - v₂)² < 4 x(1/2 a ) d
⇒ a > ( v₁ - v₂)² /2d
উত্তরঃ D)
Q17. দুই সেকেন্ডে অতিক্রান্ত দূরত্ব , h₂ = ut + 1/2 g t²
= 1/2 g x 2² ( u = 0 ) = 2 g
4 সেকেন্ডে অতিক্রান্ত দূরত্ব h₄ = 1/2 g x 4² = 8 g
6 সেকেন্ডে অতিক্রান্ত দূরত্ব h₆ = 1/ 2 g x 6² = 18 g
2 -4 সেকেন্ড সময়ের বিস্তারে অতিক্রান্ত দূরত্ব h₄ - h₂ = 8 g - 2 g = 6 g
6 -4 সেকেন্ড সময়ের বিস্তারে অতিক্রান্ত দূরত্ব h₆ - h₄ = 18 g - 8 g = 10 g
অতএব h₂ : (h₄ - h₂) : ( h₆ - h₄ ) = 2 g :6 g : 10 g = 1 : 3 :5
উত্তরঃ C)
Q18. প্রদত্ত আছে x = 40 + 12 t - t³
অতএব dx /dt = 12 - 3 t²
বাস্তুকণাটি স্থির অবস্থায় আসলে, dx/dt = 0
⇒ 3 t² = 12
বা t = 2
অতএব x = 40 + 12 x 2 - 2³ = 40 + 24 - 8 = 64 - 8 = 56
কণাটির প্রাথমিক অবস্থান , x₀ = 40 ( যেহেতু t = 0 )
স্থির অবস্থায় আসা পর্যন্ত অতিক্রান্ত দূরত্ব 56 - 40 = 16
উত্তরঃ A)
Q19.এখানে গতিবেগ , v = a √x
⇒ dx/dt = a √x
বা dx/√x = a dt
⇒ ∫ dx/√x = ∫a dt
2x ¹/² = at
⇒ x = 1/4 a² t²
উত্তরঃ C)
Q 20. n সেকেন্ডে অতিক্রান্ত দূরত্ব Sn = 1/2 a n² ( প্রাথমিক বেগ = 0 )
n তম সেকেন্ডে অতিক্রান্ত Snth = 1/2 a ( 2n - 1)
অতএব Snth/Sn = ( 2n - 1)/ n²
উত্তরঃ C)
Q21.
উওর - b)
