Determination and comparison of areas bounded by a known curve ( sin x , cos x, straight line , circle , parabola , ellipse ) by definite integration and by dividing the total enclosed area into given number of small trapezium ( i.e dividing the given interval into number of small subintervals , taking 3 values of h .
The trapezoid rule is used to approximate the area under a graph or to approximate the value of an integral .
In calculus , the trapezoidal rule is a technique for approximating the definite integral.
The trapezoidal rule works by approximating the region under the graph of the function f(x) as a trapezoid and calculating its area .
The integral can be better approximated by partitioning the integration interval ,applying the trapezoidal rule to each subinterval and summing the result .Let { xₖ } be a partition of [ a,b] such that a = xₒ< x₁< .................xₙ₋₁ < xₙ = b and △ xₖ be the length of the k-subinterval ( △ xₖ = xₖ -xₖ₋₁) then
When all △ xₖ have the same value △ x the formula becomes
Error (E) = (True value - approximate value )/True value x 100 %
The approximation becomes more accurate as the resolution of the partition increases ( that for larger n all △ xₖ decrease )
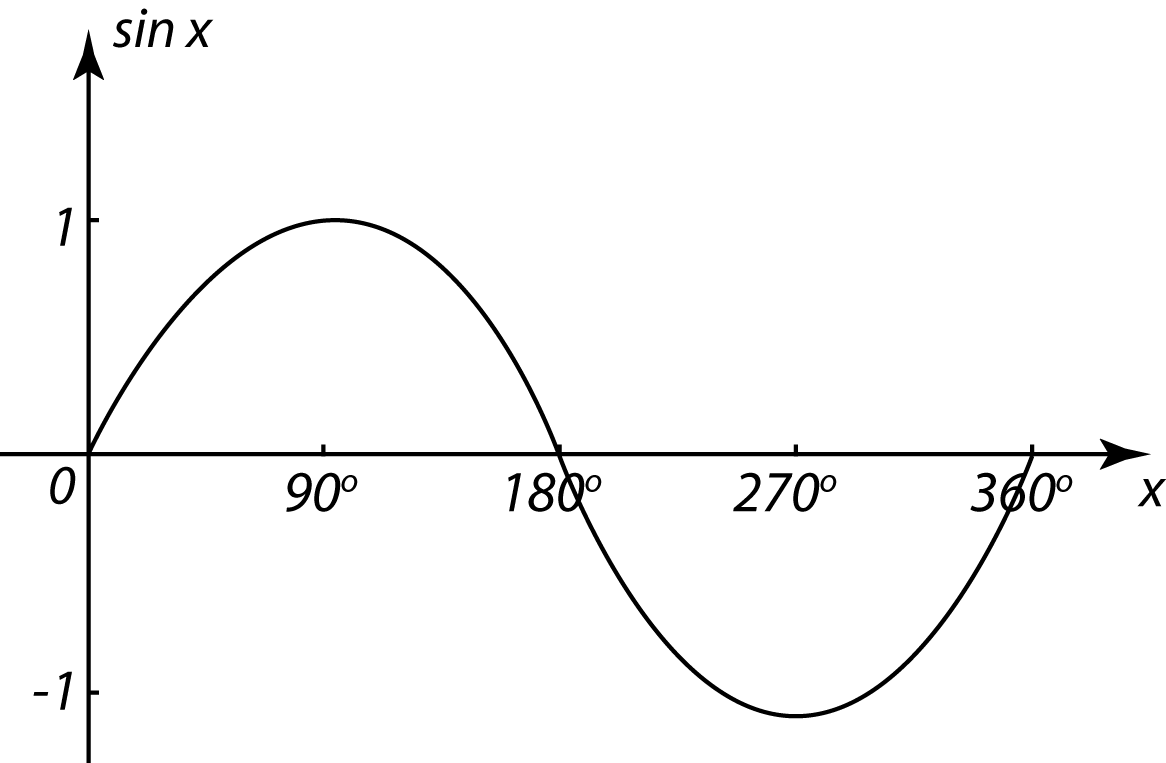
Calculation of area under f(x) = sin x curve by trapezoidal rule .
i) In this question , f(x) = sin x and let [a,b] = [0,π ] and n =10
so we get Δx=h = (b-a)/10 = π/10
The points are a=x₀ = 0 , x₁ = π/10 , x₂ = 2π/10, x₃ = 3π/10, .......................x₉ =9π/10,x₁₀ =10π/10=b
Now applying the formula for f(x) = sin x
= π/20 ( sin 0 +2 sin π/10 + 2 sin 2 π/10 + 2 sin 3 π/10 + .....................2 sin 9 π/10 + sin π )
= π/20( 0 + 0.6180 + 1.1756 + 1.6180 + 1.9021 + 2 + 1.9021 + 1.6180 +1.1756 + 0.6180 + 0 )
= π/20 ( 12.6274 ) = 1.9835
Here actual integral ( area) is
π π
⎰sin x = - cos x | = 1 + 1 = 2
0 0 ii) If we take the interval reduced to n = 5 then the points will be -
a = x₀ = 0 , x₁ = π/5 , x₂ = 2π/5, x₃ = 3π/5, x₄ = 4π/5, x₅= 5π/5= b
applying the above rule
we get the area under the cure
π/10( sin 0 + 2 sin π/5 + 2 sin 2 π/5 + 2 sin3 π/5 + 2 sin4 π/5 + sin π)
π/10( 6.1554 )
= 1.9338
Hence the error ;
∆f(x) = ( 2 - 1.9338) /2 x 100 % = 3.31 %
iii) If the intervals becomes equal to n = 7 then the points will be -
a = x₀ = 0 , x₁ = π/7 , x₂ = 2π/7 ,x₃ = 3π/7 , x₄ = 4π/7 , x₅= 5π/7 , x₆ = 6π/7 x₇ = π = b
The area under the curve sin x in the interval [ 0, π] will be -
π/14 ( sin0 + sin π/7 + 2sin 2π/7 + 2sin 3π/7 +2 sin 4π/7 + 2sin 5π/7 + 2sin 6π/7 + sin 7π/7 )
= π/14( 0 + 0.8678 + 1.5637 + 1.9499 +1.9499 + 1.5637 + 0.8678 + 0 )
= π/14 ( 8.7628 )
= 1.9664
So the error = (2 - 1.9664 )/2 x 100 % = 1.68 %
Error gets reduced when the number intervals increase . For n=10 error is minimum . for n= 5 is maximum .
Determination of the area under the curve f(x) = cos x from trapezoidal rule and its comparison with the actual value for three different values of h i.e ∆ x .
Let us take the interval-
[a,b] = [0,π/2]
i) First we take the partition corresponding to n = 5 , then the points are
a = x₀ = 0 , x₁ = π/10 , x₂ = 2π/10 , x₃ = 3π/10 , x₄ = 4π/10 , x₅ = 5π/10 = b
Applying the trapezoidal formula i.e
T = π/20( cos 0 + 2 cos π/10 + 2 cos 2π/10 + 2 cos 3π/10 + 2 cos 4π/10 + cos 5π/10 )
= π/20 ( 1+ 1.90221 + 1.61803 + 1.17557+ 0.61803 + 0 )
π/20 ( 6.31384 )
= 0.99170
π/2 π/2
Value of the actual integral = ⎰ cos x dx = sin x | = 1 - 0 = 1
0 0
error = (1-0.99170 )/1 x 100% = 0.83 %
ii) If we take partition corresponding to n = 7 then the points become ,
a = x₀ = 0 , x₁ = π/14 , x₂ = 2π/14 , x₃ = 3π/14 , x₄ = 4π/14 ,x₅ = 5π/14 , x₆ = 6π/14, x₇ = 7π/14 = b
Hence ,
T = π/28 ( cos 0 + 2cos π/14 +2cos 2π/14 + 2 cos 3π/14 + 2 cos 4π/14 + 2 cos 5π/14 + 2 cos 6π/14 + cos π/2 )
= π/28( 1 + 1.94985 + 1.80193 +1.56366 +1.24697 +0.86776 +0.44504 +0 )
= π/28 ( 8.87515 )
=0.99578
Hence error = ( actual value - calculated value )/actual value x 100 %
= (1- 0.99578) /1 x 100 % = 0.4210 %
iii) For partition corresponding to n = 10 the points are : interval = [a,b] = [0,π/2]
a = x₀ = 0 , x₁ = π/20 , x₂ = 2π/20 , x₃ = 3π/20 , x₄ = 4π/20 , x₅ = 5π/20,
x₆ = 6π/20, x₇ = 7π/20 , x₈ = 8π/20, x₉ = 9π/20, x₁₀ = 10π/20 = b
Hence under trapezoidal rule the integral becomes
T = π/40 ( cos 0 + 2cos π/20 + 2 cos 2π/20 +2 cos 3π/20 + .................+ 2cos 9π/20 + cos 10π/20 )
= π/40( 1+ 1.97537 + 1.90211 + 1.78201 +1.61803 + 1.41421 + 1.17557+ 0.90798 + 0.61803 + 0.31286 + 0 )
= π/40 ( 12.70617 )
= 0.99794
Error = ( 1- 0.99794) /1 x 100 % = 0.20 %
Importance:
Importance of Trapizoid rule is that it can help to get approx. Value of area under curve.
Especially when we do not perform the definite integration due unknown functional formula we can resort to the trapezoid rule for evaluation of the area under the curve.
Calculation of area bounded by a straight line -
the points of subintervals are :
a= x₀ = 0, x₁ = 2/5 =0.4 , x₂ = 0.8 , x₃ =1.2 , x₄ = 1.6 , x₅ = 2 =b
Applying the trapezoid rule for the interval [0,2] we get the value of the integral
T = 0.4/2 ( f(x₀) +2 f(x₁) + 2 f( x₂) + 2 f( x₃) + 2f( x₄) + f(x₅)
= 0.2 ( 0 + 1.6 + 3.2 + 4.8 + 6.4 + 4 )
=0.2 x 20
= 4
The actual value of the integral is given as
2 2 2
∫ f(x) dx = ∫ 2x dx = x²| = 4
0 0 0
Error = (actual value - value from the trapezoid rule )/actual value x 100 % = (4-4 )/4 x 100 % = 0 %
Here the error is zero because the cure is a straight line as there is no left out area between the considered trapeziums and the actual cure (straight line) . The integral is independent of partitions . So the value of the integral remain same (ie 4) for the partitions corresponding to n= 7 and n = 10 .
Calculation of area bounded by a circle :
Equation of a circle may be represented by ,
x² + y² = 5²
It can be written as ,
y² = 5² - x²
Hence , f(x) = y = √(5² - x² ) , We apply the trapezoid rule for the interval [a,b] = [0,5]
i) Let us the evaluate the area corresponding to partition , n = 5 , △x = 5/5 = 1
The points are : a = x₀ = 0, x₁ = 5/5 =1 , x₂ = 2, x₃ = 3 , x₄ = 4 , x₅ = 5
Applying the trapezoid rule -
T = △x/2 ( f(x₀) + 2f(x₁) + 2f( x₂ ) +2 f(x₃) +2f(x₄) + f(x₅) )
= 0.5( 5 + 9.79795 + 9.16515 +8 + 6 + 0 )
= 0.5 x 37.9631 =18.98155
The actual integral is :
(π x 5² )/4 = 19.63495
So, the error(Δ₁)= (19.63495 - 18.981550)/19.63495 x 100 % = 3.32 %
ii) Now let us consider the evaluation of integral for divisions n = 7 i.e △x = 5/7 = 0.71428
The points are :
From the trapezoid rule we the value of area -
T = △x/2 ( f(x₀) + 2f(x₁) + 2f( x₂ ) +2 f(x₃) +2f(x₄) +2 f(x₅) + 2f(x₆) + f(x₇)
= 0.71428/2 ( 5 + 9.89743+ 9.58315 + 9.03509 +8.20354 + 6.99418 +5.15090 + 0 )
= 0.35714 ( 53.86429 )
=19.23709
Error (Δ₂) = (19.63495 - 19.23709) /19.63495 x 100 % = 2.02 %
iii) For division corresponding to n = 10 and △x = 5/10 = 0.5
The interval points are :
From trapezoidal rule area will be -
T = △x/2 ( f(x₀) + 2f(x₁) + 2f( x₂ ) +2 f(x₃) +2f(x₄) +2 f(x₅) + 2f(x₆) +2 f(x₇) + 2 f(x₈) + 2f(x₉) + f(x₁₀) )
= 0.5/2 ( 5 + 9.94987 + 9.79795 + 9.53939 + 9.16515 + 8.66025 + 8 + 7.14142 + 6 + 4.35889 + 0 )
= 0.25 ( 77.61292 )
=19.40323
Error(Δ₃) =( 19.63495 - 19.40323)/19.63495 x100 % = 1.18 %
Obviously error gets reduced as divisions increase . as Δ₃ < Δ₂ <Δ₁
The standard equation of parabola is :
y² = 4a x
Let us take the equation y² = 4 x
Hence f(x) = y = 2 √x
Let us take the interval [a,b] = [0,4]
The integral in the interval is :
4 4 4
⎰f(x) dx = ⎰2 √x dx = 4/3 x^3/2 |
0 0 0
=4/3 ( √4³ - 0 )
(8 x 4)/3 = 32/3 = 10.66666
i) For division n= 5 i.e 🛆x = 4/5 = 0.8 ,
The points are
a= x₀ = 0, x₁ = 0.8 , x₂ = 1.6 , x₃ = 2.4, x₄ = 3.2 , x₅ = 4
The approximate value from the trapezoidal rule -
T = 🛆x/2 ( f( x₀ ) + 2f(x₁) +2f( x₂) +2f( x₃ ) + 2f( x₄ ) + f( x₅) )
= 0.8/2 ( 0 + 3.57770 + 5.05964 +6.19677 + 7.15541 +4 )
=0.4 ( 25.98952 )
= 10.39580
So the error (△ ) = (10.66666- 10.39580)/10.66666 x 100 %
= 2.539 %
ii) For n = 10 and 🛆x = 4/10 = 0.4
The partition points are -
a= x₀ = 0 , x₁ = 0.4 , x₂ = 0.8 , ----------------------+ x₉ = 3.6 . x₁₀ = 4 = b
Hence -
T = 🛆x/2 ( f( x₀ ) + 2f(x₁) +2f( x₂) +2f( x₃ ) + 2f( x₄ ) + 2 f( x₅) + ------------------+2f(x₉) + f(x₁₀) ) = 0.4/2 ( 0 + 2.52982 + 3.57770 + 4.38178 + 5.05964 + 5.65685 + 6.19677 +6.69328 + 7.15541 + 7.58946 + 4 )
= 0.2 ( 52.84071 )
= 0.2 ( 52.84071 )
= 10.56814
So the error = (10.66666 - 10.56814)/10.66666 x 100 %
= 0.92 %
iii) For division corresponding to n = 16 and 🛆x = 4/16 = 0.25
The partition points are :
a= x₀ = 0 , x₁ = 0.25 ,x₂ = 0.5 , x₃ = 0.75 , --------------------------,x₁₅ = 3.75 , x₁₆ = 4
So the estimated value -
T = 🛆x/2 ( f( x₀ ) + 2f(x₁) +2f( x₂) +2f( x₃ ) + ---------------------,2 f(x₁₅) + f( x₁₆) )
0.25/2 ( 0 + 2 +2.82842 +3.46410 + 4 + 4.47213+ 4.89897+5.29150 + 5.65685+6 +6.32455+6.63324+6.92820+ 7.21110+7.48331 +7.74596 + 4 )
= 0.125 ( 84.93833 )
= 10.61729
Hence the error = (10.66666- 10.61729)/10.66666 x100%
= 0.46 %
Now let us evaluate integral for Ellipse from Trapezoid rule .
We assume the elliptical curve as x²/9 + y²/4 = 1
⇒ y² = 4(1- x²/9)
∴ y = 2 √ (1 - x²/9) = 2/3√ (9 - x²) =f(x)
We perform the integration in the interval [a,b] = [0,3]
So the integration ,
3 3
⎰f(x) dx = ∫2/3√ (9 - x²)
0 0 3
= 2/3 [ x/2√ (9 - x²) + 9/2 sin⁻¹ x/3 ]
0
= 2/3 [ 9/2 π/2 ]
= 3/2 π = 4.71239
i) Now apply the trapezoid rule for the interval [a,b] = [0,3] and n = 5 , 🛆x = 3/5 = 0.6
f(x)= 2/3√ (9 - x²)
The partition points are given below
a = x₀ = 0, x₁ = 0.6 , x₂ = 1.2 ,x₃ = 1.8 , x₄ = 2.4 ,x₅ = 3 = b
⇒ T = 🛆x/2 ( f( x₀ ) + 2f(x₁) +2f( x₂) +2f( x₃ ) + 2f( x₄ ) + f( x₅) )
= 0.6/2 x2/3 ( 3 +5.87877 +5.49909 + 4.8 +3.6 + 0)
=0.3 x2/3 ( 22.77786)
= 4.55557
Error = (4.71239 - 4.55557 )/4.71239 x 100 % = 0.033 x100 % = 3.3 %
ii) For partitions corresponding to n = 10 , ∆x = 3/10 =0.3 , f(x)= 2/3√ (9 - x²)
Partition points are :
a = x₀ = 0, x₁ = 0.3 , x₂ = 0.6 ,,x₃ = 0.9 ,------------------------+ x₉ = 2.7 , x₁₀ = 3 =b
⇒ T = 🛆x/2 ( f( x₀ ) + 2f(x₁) +2f( x₂) +2f( x₃ ) + -----------------+2 f(x₉) +f(x₁₀)
=0.3/2 x 2/3 ( 3+ 5.96992 + 5.87877 + 5.72363 + 5.49909 + 5.19615 + 4.8 +4.28485 +3.6 +2.61533 + 0 )
= 0.1 x ( 46.56774)
= 4.656774
Error =( 4.71239 - 4.656774 )/ 4.71239 x 100 % = 1.18 %
iii) For n = 15 , ∆x = 3/15 = 0.2
Partition points are ;
a = x₀ = 0, x₁ = 0.2 , x₂ =0.4 , x₃ = 0.6 ,-------------------,x₁₄ = 2.8, x₁₅ =3 =b
⇒ T = 🛆x/2 ( f( x₀ ) + 2f(x₁) +2f( x₂) +2f( x₃ ) +------------+ 2f(x₁₄) + f(x₁₅)
= 0.2/2 x2/3(3 + 5.98665 +5.94642 + 5.87877 + 5.78273 + 5.65685 + 5.49909 + 5.30659 + 5.07543 +4.8 +4.47213 +4.07921 +3.6 + 2.99332 +2.15406 + 0)
= 0.06666 ( 70.23125 )
= 4.68161
So the Error = (4.71239 - 4.68161)/4.71239 x 100 %
= 0.65 %
Error gets reduced as the partition increases .
Inferances :
From the above discussion and examples we may come to the conclusion that for summation or integration of a function accuracy increases as the number of divisions increase in the application of trapezoid rule. Here the value we get is an approximation . But the approximation gets more closer to actual value as the number of partitions become larger .
কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন