গতি সূত্র ও ঘর্ষণ ( Laws of Motion and Friction ) :
নিউটনের প্রথম গতিসূত্র ) -
বাহির থেকে বল প্রয়োগের দ্বারা বাধ্য না করলে স্থির বস্তু চিরকাল স্থির থাকবে আর গতিশীল বস্তু চিরকাল সম বেগে সরল রেখায় গতি বজায় রাখবে ।
এই সূত্র থেকে বলের সংজ্ঞা ও বস্তুর জাড্য বা জড়তা সম্পর্কে জানতে পারা যায় ।
বল : বাহিরের থেকে কোনো বস্তুর উপর যা প্রয়োগ করলে বস্তুর স্থিতিশীল বা গতিশীল অবস্থার পরিবর্তন করে বা করতে সচেষ্ট হয় তাকে বল বলে ।
বস্তুর জড়তা : বস্তুর স্বাভাবিক প্রবণতা হল তার স্থিতিশীল বা গতিশীল অবস্থা বজায় রাখতে সচেষ্ট হয় । বস্তুর এই প্রবণতাকে তার জড়তা বা জাড্য ধৰ্ম বলে । জাড্য দুই প্রকারের । স্থিতি জাড্য এবং গতিজাড্য । স্থিতিশীল বস্তুর প্রবণতা হলো তার স্থিতিশীলতা ধর্ম বজায় রাখা - এই ধর্মকে স্থিতিজাড্য বলে । গতিশীল বস্তু সমবেগে তার গতিশীলতা ধৰ্ম বজায় রাখতে চায় - একে গতি জাড্য বলে ।
বস্তুর ভর হয় তার জাড্যের পরিমাপ । বস্তুর স্থিতিশীল বা গতিশীল অবস্থার পরিবর্তন করতে ভর ই বাধা দেয় । তাই ভরকে বস্তুর জাড্যের পরিমাপ বলে ।
নিউটনের দ্বিতীয় গতি সূত্র :
কোনো বস্তুর ভরবেগের পরিবর্তণ হলে ভরবেগ পরিবর্তনের হার বস্তুটির উপর প্রযুক্ত বলের সমানুপাতিক হয় । ভরবেগের পরিবর্তন প্রযুক্ত বলের অভিমুখে হয় ।
ভরবেগ : ভর ও বেগের সমন্বয়ে কোনো বস্তুতে যে গতির সঞ্চার হয় তাকে ভরবেগ বলে । ভর ও বেগের গুনফল দ্বারা ভরবেগ পরিমাপ করা হয় । এটি ভেক্টর রাশি ।
ভরবেগ p , ভর m এবং গতিবেগ v হলে
p = mv , ভরবেগের অভিমুখ বেগের অভিমুখে হয় ।
উপরের সমীকরণকে অবকল করে পাই ,
dp/dt = m dv/dt ( ∵ m = ধ্রুবক )
= m a ( a = dv/dt = বল প্রয়োগের ফলে সৃষ্ট ত্বরণ )
dp/dt প্রযুক্ত বল F এর সঙ্গে সমানুপাতিক
⇒ F ∝ ma
অথবা a ∝ F/m
উৎপন্ন ত্বরণ প্রযুক্ত বলের সঙ্গে সমানুপাতিক এবং ভরের সঙ্গে ব্যাস্তানুপাতিক ।
আমরা পেয়েছি, F ∝ ma
F = k ma ( k হল সমানুপাতিক ধ্রুবক ) এককের নির্বাচন দ্বারা আমরা k এর মান একক ধরতে পারি ।
মনেকরি m = 1 , a = 1 হলে F = 1 হয়।
অতএব, 1 = k .1.1
অতএব k = 1
⇒ F =ma
SI পদ্ধতিতে বলের একক নিউটন ( N ) ।
1kg ভরের বস্তুর ওপর যে বল প্রয়োগ করলে বলের অভিমুখে 1 m/s² ত্বরণ সৃষ্টি হয় সেই পরিমাণ বলকে এক নিউটন বলে । বলের মাত্রা [MLT⁻² ]
নিউটনের তৃতীয় গতিসূত্র :
যখনই কোনো বস্তু অন্য কোনো দ্বিতীয় বস্তুর ওপর বল(ক্রিয়া ) প্রয়োগ করে তখন দ্বিতীয় বস্তুও প্রথম বস্তুর একটি সমান ও বিপরীত মুখী বল(প্রতিক্রিয়া ) প্রয়োগ করে । অথবা প্রত্যেক ক্রিয়ার একটি সমান ও বিপরীত প্রতিক্রিয়া আছে । ক্রিয়া ও প্রতিক্রিয়া ভিন্ন বস্তুর উপর কাজ করে । প্রতিক্রিয়া বাদদিয়ে কোনো ক্রিয়া হয় না ।
বলের ঘাত (Impulse ) :
মনে করি একই সরল রেখায় গতিশীল A ও B বস্তু দুটি র মধ্যে সংঘর্ষ ঘটে । সংঘর্ষের ক্রিয়া কাল t ,অর্থাৎ t সময় ধরে বস্তুদুটির সংস্পর্শ ঘটে এবং ভর বেগের পরিবর্তন ঘটে । সংঘর্ষের পরে ভিন্ন বেগে একই সরল রেখায় গমন করে ।
প্রযুক্ত বলের গড় মান ও উহার ক্রিয়া কালের গুণফলকে বলের ঘাত বলে ।
অর্থাৎ I = F .t = △p ( I = বলের ঘাত, △p = ভরবেগের পরিবর্তন )
বলের ঘাত একটি ভেক্টর রাশি । এর একক kg m s⁻¹ বা N. s
ত্বরিত ও অত্বরিত নিৰ্দেশ তন্ত্র ( Non-inertial and Inertial Frames) ;
আমরা জানি গতি এবং স্থিতি আপেক্ষিক । পরম স্থিতি ও পরম গতিশীল বলে কিছু হয় না । বস্তুর অবস্থান বা তার গতীয় অবস্থা বিভিন্ন নিৰ্দেশ তন্ত্র অনুসারে বিভিন্ন হতে পারে । যেমন যাত্রীরা এবং চলন্ত ট্রেনের ভিতরে অবস্থিত সবকিছু ট্রেনের সাপেক্ষে স্থির থাকে ,কিন্তু প্লাটফর্মের সাপেক্ষে যাত্রীরা এবং ট্রেনের ভিতরের সবকিছু গতিশীল থাকে । অনুরূপভাবে কোনো বস্তুকে চলন্ত ট্রেনের জানালা থেকে ফেলে দিলে যাত্রীর সাপেক্ষে বস্তুটির গতিপথ সোজা নিম্নাভিমুখে সরলরৈখিক মনে হবে । কিন্তু ট্রেনের বাহিরে অবস্থিত কোনো ব্যক্তির সাপেক্ষে গতিপথ অধি বৃত্তাকার মনে হবে ।
নিউটনের প্রথম গতিসূত্র সমস্ত নিৰ্দেশতন্ত্রে(Reference Frame ) প্রযোজ্য নয় । যে নিৰ্দেশতন্ত্রে সূত্রটি প্রযোজ্য সেই নিৰ্দেশ তন্ত্রকে অত্বরিত নিৰ্দেশ তন্ত্র( Inertial Frames) বলে । এই ধরণের নিৰ্দেশতন্ত্র দূরবর্তী নক্ষত্র এর সাপেক্ষে স্থির বা সমবেগে গতিশীল থাকে । অর্থাৎ যেসকল নিৰ্দেশতন্ত্রের ত্বরণ নেই বা সমবেগে গতিশীল সেই সকল নিৰ্দেশতন্ত্রকে অত্বরিত নিৰ্দেশ তন্ত্র( Inertial Frames) বলে ।
মনেকরি একটি নিৰ্দেশতন্ত্র S¹ অপর একটি নিৰ্দেশ তন্ত্র S এর সাপেক্ষে স্থির বেগে গতিশীল নয় , S¹ নিৰ্দেশতন্ত্র S এর সাপেক্ষে বৃত্তপথে ঘুরছে । অর্থাৎ S¹ , S এর সাপেক্ষে ত্বরণ যুক্ত গতিতে আছে । একটি বস্তু যা S এর সাপেক্ষে স্থির থাকে তা S¹ এর সাপেক্ষে বৃত্তাকার গতিতে আছে বলে মনে হবে । অর্থাৎ বস্তুটিকে ত্বরিত মনে হবে S¹ এর সাপেক্ষে । সুতরাং S এর সাপেক্ষে বস্তুটির উপর কোনো বল কাজ করে না ,কিন্তু S¹ সাপেক্ষে একটি অলীক বা কাল্পনিক বল ( অভিকেন্দ্র বল ) ক্রিয়া করবে । এর অর্থ হলো নিউটনের প্রথম দুটি গতিসূত্র S¹ নিৰ্দেশতন্ত্রে প্রযোজ্য বা ঠিক থাকবে না । যে সকল নিৰ্দেশতন্ত্রে নিউটনের প্রথম দুটি সূত্র প্রযোজ্য নয় বা ঠিক থাকে না তাকে ত্বরিত নিৰ্দেশ তন্ত্র (Non-inertial Frame )বলে ।
ঘর্ষণ ( Friction) :
যখন একটি বস্তু অপর একটি বস্তুর উপর পিছলে যায় বা গড়িয়ে চলে তখন উভয়ের স্পর্শতলে উদ্ভূত একটি স্পর্শকীয় বল গতির বিরুদ্ধে ক্রিয়া করে । এই বলকে ঘর্ষণ বলে ।
সর্বোচ্চ ঘর্ষণবল যখন একটি বস্তু কোনো তলের উপর গতিশীল হবার উপক্রম হয় তখন সেই ঘর্ষণবলকে স্থিতঘর্ষণ এর সীমাস্ত মান ( Limiting Friction)বলে । স্থিত ঘর্ষণ গুণাঙ্ক μₛ হলে
μₛ = fₛ/R (R লম্ব প্রতিক্রিয়া যা স্পর্শ তলের উপর লম্বভাবে কাজ করে )
একটি বস্তুকে অপর একটি বস্তুর উপর বা কোনো তলের উপর স্থির বেগে চালু থাকলে যে ঘর্ষণ বল গতির বিপরীতে কাজ করে তাকে চল ঘর্ষণ (Kinetic Friction )বলে | চল ঘর্ষণ গুণাঙ্ক kₖ হলে
kₖ = fₖ/R
kₖ সর্বদাই μₛ অপেক্ষা কম । অর্থাৎ চল ঘর্ষণের মান স্থিত ঘর্ষণ অপেক্ষা কম ।
ঘর্ষণ কোণ (Angle of Friction) :
ঘর্ষণ বলের সীমাস্থ মান ও লম্ব প্রতিক্রিয়ার লব্ধি লম্ব প্রতিক্রিয়ার সঙ্গে যে কোণ করে তাকে ঘর্ষণ কোণ বলে ।
tanθ = f/R = μ
⇒ θ = tan⁻¹ ( μ)
বিরাম কোণ ( Angle of Repose ) :
মনেকরি একটি বস্তু একটি নত তলের উপর রক্ষিত আছে । নত তলের উন্নতি কোণ ক্রমশ বৃদ্ধি করা হলে একটি নিৰ্দিষ্ট কোণে বস্তুটি পড়তে শুরু করবে । অর্থাৎ নত তলের যে সর্বনিম্ন কোণে নত তলের উপর রক্ষিত বস্তু পড়তে শুরু করে সেই কোণকে বিরামকোণ বলে ।
ঘর্ষণের সীমাস্ত মান ( f) = mg sin α
লম্ব প্রতিক্রিয়া (R) = mg cos α
tan α = f/R = μ = tan θ
α = θ = tan⁻¹ ( μ)
মুক্ত বস্তুচিত্রের দ্বারা মেকানিক্স এ র সমস্যার সমাধান ( Solving Problems in Mechanics by Free body Diagram) :
এই ধরনের সমস্যায় একাধিক বস্তু পরস্পর সুতা ,তার ,স্প্রিং বা চক্রের দ্বারা যুক্ত থাকে । প্রত্যেক বস্তুর উপর ক্রিয়াশীল বলগুলি হিসাব করে প্রতিটি বস্তুর জন্য ভিন্ন ভিন্ন গতিও সমীকরণ তৈরি করা হয় । পরে সমীকরণগুলি সমাধান করে সমস্যাটির সমাধান করা হয় । সমস্যার সমাধানের জন্য রেখাচিত্র অঙ্কন করা হয় যেখানে প্রত্যেকটি বস্তুর ওপর কি কি বল ক্রিয়া করে তা স্পষ্টভাবে উল্লেখ থাকে ।
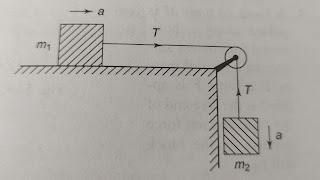
1. ঘর্ষণহীন চাকার উপর রক্ষিত একটি তারের দুই প্রান্তে বাঁধা দুটি বস্তুর গতি :
মনেকরি একটি তার একটি ঘর্ষণহীন চাকার উপর রাখা আছে । তারের দুই প্রান্তে m₁ ও m₂ ভর সংযুক্ত আছে এবং m₁> m₂ । যখন বস্তু দুটিকে ছেড়ে দেওয়া হবে m₁ ভর নীচের দিকে এবং m₂ ভর উপরের দিকে গতিশীল হবে । মনে করি তারটির ভর নগন্য । m₁ ভরের বস্তুর গতির সমীকরণ হবে -
m₁g - T = m₁ a ( T তারের টান , a ত্বরণ ) অনুরূপে m₂ ভরের বস্তুর সমীকরণ হবে -
T - m₂ g = m₂ a
উপরের দুই সমীকরণ সমাধান করে পাই
a = ( m₁ - m₂) g/( m₁ + m₂)
এবং T = 2 m₁ m₂ g /(m₁ + m₂)
2. ঘর্ষণহীন টেবিলে পরস্পর স্পর্শকরে রক্ষিত দুটি বস্তুর গতি :
চিত্রে দুটি ভর m₁ এবং
m₂ একটি ঘর্ষণহীন টেবিলের উপর রক্ষিত । চিত্রে যেমন দেখানো হয়েছে F বল
m₁ এর উপর প্রযুক্ত হয়েছে । সংস্থাটির ত্বরণ a হলে ,
a = F/(m₁ + m₂)
m₂ ভরের উপর স্পর্শ বল F₂ হলে ,
F₂ = m₂F/((m₁ + m₂)
3. ঘর্ষণহীন টেবিলে স্পর্শকরে একটি বস্তুর পরে আর একটি বস্তু রক্ষিত এরূপ তিনটি বস্তুর গতি :
ধরি একটি টেবিলের উপর তিনটি বস্তু স্পর্শকরে চিত্রের মতো করে আছে । বস্তু তিনটির ভর যথাক্রমে m₁ , m₂ এবং m₃ | m₁ভরের উপর F বল প্রযুক্ত হয়েছে । সংস্থাটির ত্বরণ a হলে
a = F/(m₁ + m₂ + m₃)
m₂ এবং m₃ ভরের উপর স্পর্শ বল যথাক্রমে ,
F₂ =(m₂ + m₃ )F/(m₁ + m₂ + m₃)
এবং F₃ = m₃F/(m₁ + m₂ + m₃)
4.ঘর্ষণহীন টেবিলের উপর তার দ্বারা সংযুক্ত দুটি বস্তুর গতি :
চিত্রে যেমন দেখানো হয়েছে m₂ ভরের বস্তুর উপর F বল প্রযুক্ত হয়েছে ।
মনেকরি তারের টান T হলে m₁ ও m₂ ভরের গতির সমীকরণ হবে
m₁a = T
m₂a = F - T
উপরের দুই সমীকরণ যোগ করে পাই
a = F/(m₁ + m₂)
তারের টান ,
T = m₁a = m₁F/(m₁ + m₂)
m₁ ভরের উপর ক্রিয়াশীল বল
F₁ = m₂F/(m₁ + m₂)
যদি F বল m₁ ভরের উপর কাজ করে তাহলে
a = F/(m₁ + m₂)
এবং T = m₂a
m₂ এর উপর ক্রিয়াশীল বল
F₂ = m₁F/(m₁ + m₂)
5. মসৃণ টেবিলের উপর অবস্থিত তার দ্বারা সংযুক্ত তিনটি বস্তুর গতি :
মনেকরি তিনটি বস্তুর ভর হল -
m₁ , m₂ এবং m₃
| m₁ ভরের বস্তুর উপর প্রযুক্ত বল F |
সংস্থাটির ত্বরণ হবে ,
a = F/(m₁ + m₂ + m₃)
m₂ এবং m₃ ভরের বস্তুর উপর ক্রিয়াশীল বল যথাক্রমে
F₂ = ( m₂ + m₃)F/(m₁ + m₂ + m₃)
এবং F₃ = m₃ F/(m₁ + m₂ + m₃)
6.দুটি বিভিন্ন ভর একটি ভরহীন তার দ্বারা সংযুক্ত এবং একটি অবলম্বনের থেকে ঝুলন্ত আছে ।
m₂ ভরের উপর F বল নিচের দিকে প্রয়োগ করা হয়েছে । m₁ এবং m₂ মধ্যেবর্তী তারের টান T হলে T = F + m₂ g
অবলম্বন ও m₁ ভরের মধ্যে টান T′ = F + (m₁ + m₂)
7. ঘর্ষণহীন নততলের উপর রক্ষিত বস্তুর গতি -
মনে করি θ কোণে আনত AB নত তলের উপর একটি বস্তু রক্ষিত আছে । AC = h | নত তল বরাবর অভিকর্ষজ ত্বরণের উপাংশ g sinθ | mgcosθ উপাংশ নত তলের লম্ব প্রতিক্রিয়া R এর সঙ্গে সমান হবে ।
যদি বস্তুটিকে A বিন্দু থেকে ছেড়ে দেওয়া হয় তাহলে ভূমির B বিন্দুতে পৌঁছানোর সময় বেগ v হলে
v² = 0 + 2 a s
= 2 g sinθ L ( L = নত তলের দৈর্ঘ্য = AB )
= 2gh ( ∵ h = Lsinθ )
∴ v = √(2gh)
B বিন্দুতে পৌঁছাতে সময় t লাগলে
v = at
⇒ t = v/a = √(2gh)/(g sinθ)
t = 1/sinθ√(2h/g)
8. ভরহীন তার দ্বারা যুক্ত দুটি বস্তুর একটি ঘর্ষণ হীন টেবিলে রক্ষিত অপরটি টেবলের প্রান্তে একটি চাকার মাধ্যমে ঝুলন্ত আছে ।
মনেকরি সংস্থাটির ত্বরণ a |
টেবিলের উপর রক্ষিত বস্তুর গতীয় সমীকরণ
T = m₁ a ( T = তারের টান )
ঝুলন্ত বস্তুটির সমীকরণ ,
m₂ g -T = m₂ a
উভয় সমীকরণ সমাধান করে পাই ,
a =m₂ g /(m₁ + m₂)
T = m₁ a
= m₁ m₂ g /(m₁ + m₂)
টেবিল ঘর্ষণহীন হলে m₂ ∠ m₁ হলেও m₁ গতিশীল হবে ।
9.একটি তারের দুই প্রান্তে দুটি ভর যুক্ত এবং তারটি একটি ঘর্ষণহীন নত তলের উপর প্রান্তে অবস্থিত একটি চাকার উপরে রক্ষিত :
নত তলের উপর রাখা বস্তুটির গতির সমীকরণ -
T - m₁g sinθ = m₁ a ( m₁ ভর নত তলের উপরের দিকে a ত্বরণে উঠছে )
কপিকলের উপর ঝুলন্ত বস্তুটির গতির সমীকরণ -
m₂ g -T = m₂ a
উপরের সমীকরণ দুটি সমাধান করে পাই ,
a = ( m₂ - m₁ sinθ) g/( m₁ + m₂)
এবং T = m₂ g -m₂ a = m₂ ( g - a)
যদি m₁ ভর নত তল বরাবর নীচের দিকে নামে তাহলে গতির সমীকরণ হবে -
m₁g sinθ -T = m₁ a
এবং
T - m₂ g = m₂ a
সমাধান করে পাই ,
a = (m₁ sinθ - m₂)g/(m₁ + m₂)
T = m₂(g + a)
10. ভরহীন তারের দ্বারা দুইটি ব্লক যুক্ত আছে এবং তারটি একটি ঘর্ষণহীন দ্বীনত তলের উপরে কপিকলের উপর রক্ষিত ।
মনেকরি m₁ ভর টি উপরের দিকে উঠছে । এই অবস্থায় m₁ ভরের গতির সমীকরণ -
T - m₁ g sinθ₁ = m₁ a ( a = ত্বরণ )
m₂ ভরের গতির সমীকরণ -
m₂ g sinθ₂ -T = m₂ a
উপরের সমীকরণ দুটি থেকে T অপনয়ন করে পাই ,
a = (m₂ sinθ₂ - m₁ sinθ₁)g/(m₁ + m₂)
এবং T = m₁(a + g sinθ₁) = m₂(g sinθ₂ -a)
বহু বিকল্প ভিত্তিক প্রশ্না বলি (MCQ):
1.0.5 kg ভরের একটি ক্রিকেট বল 30 m/s বেগে লম্ব ভাবে ব্যাটে আঘাত করে ।বিপরীত দিকে 20 m/s বেগে বলটি ফিরে আসে । ব্যাটের উপর প্রযুক্ত বলের ঘাত কত ?
a) 0.5 Ns b) 1.0 Ns
c) 25 Ns d) 50 Ns
2.
m₁ ও m₂ ভরের দুটি বস্তু তার দ্বারা ঘর্ষণহীন দুটি কপিকলের মাধ্যমে m ভরের সঙ্গে চিত্র অনুযায়ী যুক্ত ।
যদি
m₁ ও m₂ ভর v বেগে নীচের দিকে নামে তাহলে m ভর কত বেগে উপরে উঠবে ?
a) v b) √2 v
c) √3v d) 2 v
3. m এবং 2m ভরের দুটি বস্তু কপিকলের মাধ্যমে চিত্রের মত করে যুক্ত । যখন 2m ভরকে ছেড়ে দেওয়া হবে তখন m ভর কত ত্বরণে উপরে উঠবে ?
a) g/3 b ) g/2
c) g d) 2g
4. নীচের চিত্রে যদি তারটির মুক্ত প্রান্তে F =2 mg বলে টানা হয় তাহলে m ভর কত ত্বরণে উপরে উঠবে ?
a) g/3 b ) g/2
c) g d) 2g
a) FM/(M + m) b) Fm/(M + m
c) FM/(M - m) d) F
6. θ কোণে আনত একটি নত তলের উপরে অবস্থিত একটি বস্তু আছে । নত তলটি একটি লিফটের ভিতরে আছে । লিফটি যদি a মন্দনে নীচের দিকে নামে তাহলে নত তল বরাবর বস্তুর উপর কত ত্বরণ কাজ করবে ?
a) g sin θ b) a sin θ
c) ( g - a) sin θ d) ( g + a) sin θ
7. একটি ব্লক 45º কোণে আনত একটি মসৃণ নত তল বরাবর পড়তে যে সময় লাগে ওই একই কোণে আনত অমসৃণ তল বরাবর পড়তে তার দ্বিগুণ সময় লাগে । অমসৃণ তলটির চল ঘর্ষণ গুণাঙ্ক কত ?
a) 0.25 b) 0.5
c) 0.75 d) 1.0
8. θ কোণে আনত একটি নত তলের উপরের অর্ধাংশ মসৃণ কিন্তু নীচের অর্ধাংশ অমসৃণ । একটি বস্তু নত তলের উপরের বিন্দু থেকে স্থিরঅবস্থা থেকে যাত্রা শুরু করে নত তলের নিচে আবার স্থির অবস্থায় আসে । নত তলের শেষ অর্ধাংশের ঘর্ষণ গুণাঙ্ক কত ?
a) μ = 2 tan θ b) μ = tan θ
c) μ = 2 /tan θ d) μ = 1/ tan θ
9.বালি ভর্তি একটি ট্রাক মসৃণ রাস্তায় u সুষম গতিতে চলছে । যদি ট্রাকের তলার একটি ছিদ্র দিয়ে △m ভরের বালি △t সময়ে পড়ে যায় তাহলে ট্রাকটির u সুষম গতি বজায় রাখার জন্য কত বলের প্রয়োজন ?
a) △mu/△t b) △mu/2△t
c) △mu²/△t d) zero
10. m₂ ভরের একটি ব্লক একটি মসৃণ টেবিলের উপর আছে । ব্লকটিকে একটি তারের দ্বারা টেবিলের প্রান্তে আটকানো কপিকলের মাধ্যমে m₁ ভর ঝোলানো আছে । যদি m₁ > m₂ তাহলে সংস্থাটির ত্বরণ কত ?
a) m₁g / m₂ b) m₂g/m₁
c) m₁g /(m₁ + m₂) d) m₂ g/(m₁ + m₂)
11.m₁ ভরের A বস্তু একটি মসৃণ টেবিলের উপর আছে । অপর একটি বস্তু B , ভর m₂ ,A বস্তুর সংস্পর্শে আছে । A বস্তুর উপর F বল প্রয়োগ করা হল । B বস্তুর উপর A দ্বারা প্রযুক্ত বল কত ?
a) .m₁/m₂ F b) m₂/m₁ F
c) m₁ F /(m₁ + m₂) d) m₂ F/(m₁ + m₂)
12. A এবং B দুই ব্যক্তি একটি মসৃণ তলে 6 m দূরত্বে দাঁড়িয়ে আছে । A ,B এর ভর যথাক্রমে 50 kg এবং 70 kg । তারা পরস্পরকে একটি দড়ি দিয়ে টানছে । A, B যখন পরস্পর মিলিত হবে তখন কে কত দূরত্ব যাবে ?
a) উভয়েই 3 m করে দূরত্ব যাবে ।
b) A যাবে 4 m এবং B , 2 m যাবে ।
c) A যাবে 2.5 m এবং B যাবে 3.5 m |
d) A যাবে 3.5 m এবং B যাবে 2.5 m |
13.এক ব্যক্তি ইঞ্জিনের দিকে মুখ করে ট্রেনের ভিতরে বসে আছে । সে একটি মুদ্রা টস করলো । মুদ্রাটি তার পিছনে পড়ল । এর অর্থ হল - ট্রেনটি
a) নিৰ্দিষ্ট ত্বরণে সামনের দিকে চলছে ।
b) নিৰ্দিষ্ট মন্দনে সামনের দিকে চলছে ।
c) সম বেগে সামনের দিকে চলছে ।
d) সম দ্রুতিতে পিছনের দিকে চলছে ।
14.W = Mg ওজনের এক ব্যক্তি একটি লিফটে দাঁড়িয়ে আছে । লিফটি a ত্বরণে উপরের দিকে উঠেছে । যদি g অভিকর্ষজ ত্বরণ হয় তাহলে লোকটির আপাত ওজন কত ?
a) W(1 + a/g) b) W(1 - a/g)
c) W d) zero
15. একটি স্প্রিং ব্যালান্সের এক প্রান্তে 10 N বল প্রয়োগ করা হল । ওপর প্রান্তেও 10 N বল প্রয়োগ করা হল । স্প্রিং তুলার পাঠ কত হবে ?
a) zero b) 5 N
c) 10 N d) 20 N
16. একটি ব্লক A কে একটি মসৃণ নত তল এর উপর থেকে ছেড়ে দেওয়া হল । একই সময়ে ওপর একটি ব্লক B কে সরাসরি নত তলের উপর প্রান্ত থেকে উলম্ব ভাবে ফেলে দেওয়া হলো । নীচের কোন বিবৃতি গুলি সঠিক ?
a) দুটি ব্লকই একই সময়ে ভূমিতে পড়বে ।
b) A ব্লক B ব্লক থেকে আগে ভূমিতে পড়বে ।
c) উভয় ব্লকই একই দ্রুতিতে মাটিতে পড়বে ।
d) ব্লক B ,ব্লক A থেকে বেশি দ্রুতিতে মাটিতে পড়বে ।
17. একটি নত তলের শীর্ষ বিন্দু থেকে একটি ব্লককে ছেড়ে দেওয়া হল । নত তলের নতি কোণ θ হলে ব্লকটির ভূমিতে পৌঁছাতে কত সময় লাগবে ?
a) √(2h/g) b) sinθ√(2h/g)
c) 1/sinθ√(2h/g) d) 1/cosθ√(2h/g)
18.M ভরের একটি ব্লক একটি নত তলের উপরে আছে । নত তলটির নতি ক্রমশ বৃদ্ধি করা হলে যখন নতি θ হয় তখন ব্লকটি পিছলে পড়া শুরু করে । নত তল বরাবর কত সর্বনিম্ন বল (F) প্রয়োগ করলে ব্লকটি উপরের দিকে উঠবে ?
a) Mg sin θ b) Mg cos θ
c) 2Mg cos θ d) 2 Mg sin θ
19. 200 g ভরের একটি বস্তু x অক্ষের ধনাত্বক 5 m/s গতিশীল আছে । একটি ধ্রুবক মানের 0.4 N বল x অক্ষের ঋনাত্বক দিকে 10 s ধরে ক্রিয়াশীল । t = 2.5 s বস্তুটির অবস্থান কোথায় হবে ?
a) x = 1.0 m b) x = 1.25 m
c) 1.5 m d) 1.75 m
20. 19 নং প্রশ্নে t = 2.5 s বস্তুটির গতিবেগ কত হবে ?
a) 7.5 m s⁻¹ b) 6.25 m s⁻¹
c) 5.0 m s⁻¹ d) zero
21. 19 নং প্রশ্নে t =30 s বস্তুটির অবস্থান কোথায় হবে ?
a) x = - 350 m b) x = -400 m
c) x = -450 m d) x = - 500 m
22. 19 নং প্রশ্নে t = 30 s সময়ে বস্তুটির দ্রুতি কত হবে ?
a) 10 m s⁻¹ b) 15 m s⁻¹
c) 20 m s⁻¹ d) 25 m s⁻¹




















কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন