প্রাস ( Projectile) :
কোনো প্রক্ষিপ্ত বস্তুর অভিকর্ষের অধীনে গতিকে প্রাস বলে । যেমন - কোনো বাড়ির ছাদ থেকে নিক্ষিপ্ত বস্তুর গতি , রাইফেল থেকে প্রক্ষিপ্ত বুলেটের গতি , এরোপ্লেনে থেকে ফেলে দেওয়া বোমার গতি বা কোনো খেলোয়াড় দ্বারা নিক্ষিপ্ত জ্যাভেলিনের গতি ইত্যাদি হলো প্রাসের উদাহরণ । প্রাসের গতি দুই রকমের হতে পারে । ( i) নিৰ্দিষ্ট উচ্চতা থেকে অনুভূমিক ভাবে ছোঁড়া বস্তুর গতি । (ii) ভূমি থেকে তীর্যক ভাবে নিক্ষিপ্ত বস্তুর গতি ।
(i) নিৰ্দিষ্ট উচ্চতা থেকে অনুভূমিক দিকে নিক্ষিপ্ত বস্তুর গতি -
যদি t = 0 সময়ে ভূমি থেকে খানিক উচ্চতা থেকে v₀ অনুভূমিক বেগে ছোঁড়া হল । t সময় পরে বস্তুটির অনুভূমিক দিকে x দূরত্ব এবং উলম্ব দূরত্ব y অতিক্রম করলে ,
x = v₀ t এবং y = - 1/2 g t²
উপরের সমীকরণ থেকে t অপনয়ন করে পাই ,
y = - 1/2 g x²/ v₀² = k x² ( যেখানে k = - 1/2 g / v₀² )
⇒ y = k x² , এটি একটি অধিবৃত্তের সমীকরণ ।
অতএব অনুভূমিক ভাবে নিক্ষিপ্ত বস্তুর গতিপথ অধিবৃত্তাকার হয় ।
লব্ধি বেগ:
t সময় পরে নিক্ষিপ্ত বস্তর গতিবেগ v হলে,
v =√ (v₀² + g²t²)
যদি লব্ধিবেগ উলম্ব দিকের সঙ্গে α কোন করলে
tan α = v₀/gt
ii) অনুভূমিকের সঙ্গে কোণ করে নিক্ষিপ্ত বস্তুর গতি :
যদি v₀ বেগে অনুভূমিকের সঙ্গে θ কোণ করে নিক্ষিপ্ত হলে t সময় পরে অনভূমিক ও উলম্ব দিকে অতিক্রান্ত দূরত্ব
x =( v₀ cos θ ) t
এবং y =( v₀ sin θ )t - 1/2 g t²
উপরের সমীকরণ থেকে t অপনয়ন করে পাই ,
y = px - qx² , যেখানে p = tan θ , q = g/( 2v₀² cos²θ ) হলো ধ্রুবক । এটি হলো একটি অধিবৃত্তের সমীকরণ । সুতরাং কোনো নিক্ষিপ্ত বস্তুর গতিপথ একটি অধিবৃত্ত হয় ।
সর্বোচ্চ উচ্চতা : সর্বোচ্চ উচ্চতা H হলে
0 = v₀² sin² θ - 2H g ( সর্বোচ্চ উচ্চতায় উলম্ব গতিবেগ 0 )
∴ H = v₀²sin² θ/2g
উড্ডয়ন কাল( Flight Time ):
নিঃক্ষেপ বস্তুটি যে সময় কাল ধরে বায়ুতে থাকে সেই সময়কে উড্ডয়ন কাল বলে । সর্বোচ্চ উচ্চতায় উঠতে t₁ সময় লাগলে
0 = v₀ sin θ - g t₁
⇒ t₁ = v₀ sin θ /g
উড্ডয়ন কাল T হলে ,y =( v₀ sin θ )t - 1/2 g t² থেকে পাই ,
0 = ( v₀ sin θ ) T - 1/2 g T²
⇒ T = ( 2v₀ sin θ )/g
অনুভূমিক পাল্লা (Horizontal Range):
নিক্ষেপ বিন্দু থেকে অনুভূমিক দিকে সর্বোচ্চ অতিক্রান্ত দূরত্বকে পাল্লা বলে ।
পাল্লা = অনুভূমিক বেগ x উড্ডয়ন কাল
= ( v₀ cos θ ) x T
= ( v₀ cos θ ) x ( 2v₀ sin θ )/g
R = v₀² sin 2θ /g
R এর মান সর্বোচ্চ হবে যদি sin 2θ = 1 হয়
অর্থাৎ 2θ = 90⁰
বা ,θ = 45⁰
R এর সর্বোচ্চ মান v₀² /g
অতএব কোনো বস্তুকে অনুভূমিকের 45⁰ কোণ করে ছুঁড়লে সর্বোচ্চ অনুভূমিক দূরত্ব যাবে ।
উড্ডয়ন কাল ও একটি নততলের উপর পাল্লা :
মনেকরি নততল OAB অনুভূমিকের উপর α কোণ করে । একটি বস্তুকে অনুভূমিকের সঙ্গে θ কোণ করে v₀ বেগে ছোঁড়া হলো । x - অক্ষ OA বরাবর বিস্তারিত এবং y - অক্ষ OA সমতলের উপর লম্ব । মনে করি নিক্ষিপ্ত বস্তুটি P বিন্দুতে নত তলকে আঘাত করে । নত তল বরাবর পাল্লা হল R = OP | গতিবেগের x এবং y উপাংশ গুলি যথাক্রমে ,
vₓ = v₀ cos (θ - α ) এবং vₕ = v₀ sin( θ - α )
অভিকর্ষ ত্বরণের x এবং y উপাংশ গুলি যথাক্রমে
- g sin α এবং - g cos α
T হল নততলের উপর উড্ডয়ন কাল।
যেহেতু T সময়ে অতিক্রন্ত উলম্ব দূরত্ব 0 ( h = 0 )
0 = vₕT - 1/2 g cos α T²
অতএব 0 = vₕ -1/2 g cos α T
0 = v₀ sin ( θ - α ) - 1/2 g cos α T
T = 2 v₀ sin ( θ - α ) / g cos α
উড্ডয়ন কালে বেগের অনুভূমিক উপাংশ v₀ cos θ ধ্রুবক থাকে ।
অনুভূমিক দূরত্ব OQ = v₀ cos θ T
এখন OQ/ OP = cos α
অতএব OP = OQ /cos α = v₀ cos θ T / cos α
= v₀ cos θ 2 v₀ sin ( θ - α ) /( g cos α cos α )
অতএব, R= 2 v₀² sin ( θ - α ) cos θ /(g cos² α )
কৌণিক বেগ ও কৌণিক ত্বরণ :
সম কৌণিক গতিতে ঘূর্ণনশীল বস্তুর ব্যাসার্ধ ভেক্টর প্রতি সেকেন্ডে যে কোণে ঘুরে যায় তাকে কৌণিক বেগ বলে । যদি ব্যাসার্ধ ভেক্টর △t সময়ে △θ কোণে আবর্তিত হয় তাহলে কৌণিক বেগ হবে -
ω = lim ( △θ / △t ) = dθ/dt
△t →0
ω কে rad s⁻¹ এককে প্রকাশ করা হয় ।
রৈখিক বেগ ও কৌণিক বেগের মধ্যে সম্পর্কটি নিম্নরূপ
v = r ω ( r = বৃত্তিও গতির ব্যাসার্ধ )
রেডিয়ান ( radian ) : বৃত্তের ব্যাসার্ধের সমান চাপ কেন্দ্রে যে কোণ উৎপন্ন করে তাকে রেডিয়ান বলে ।
রেডিয়ান (θ ) = বৃত্ত চাপ (s)/ব্যাসার্ধ (r ) ,
কৌণিক ত্বরণ :
কৌণিক বেগের পরিবর্তনের হারকে কৌণিক ত্বরণ বলে ।
কৌণিক ত্বরণ ( α ) = dω/dt
রৈখিক ত্বরণ(a) ও কৌণিক ত্বরণের মধ্যে সম্পর্কটি :
a = r α কৌণিক ত্বরণের একক rad s⁻²
সুষম বৃত্তিও গতি (Uniform Circular Motion): এক্ষেত্রে একটি বস্তুকণা সমদ্রুতিতে বৃত্তাকার পথে ঘূর্ণন শীল থাকে । বাস্তুকণাটির বেগের মানের কোনো পরিবর্তন হয় না । কিন্তু বেগের অভিমুখের অনবরত পরিবর্তণ ঘটে । ফলে একটি ত্বরণ দেখা দেয় । এই ত্বরণ বৃত্তটির কেন্দ্রের অভিমুখে কাজ করে । এই ত্বরণকে অভিকেন্দ্র ( Centripetal Acceleration) ত্বরণ বলে । সম দ্রুতিতে ঘূর্ণায়মান বস্তুকণার ওপর ক্রিয়াশীল যে ত্বরণ বৃত্তের কেন্দ্রের অভিমুখে কাজ করে তাকে অভিকেন্দ্র ত্বরণ বলে । এই ত্বরণের মান হয় -
a = v²/r ( r = বৃত্তপথের ব্যাসার্ধ , v = বস্তুকণাটির দ্রুতি )
বৃত্তের পরিধি বরাবর বস্তুকণাটির এক বার ঘুরতে T সময় নিলে ,
T = 2 π r /v , T কে পর্যায় কাল বলা হয় ।
অভিকেন্দ্র ত্বরণের ( a = v²/r ) প্রমাণ :
ধরি একটি বস্তুকণা r ব্যাসার্ধের বৃত্তপথে v বেগে ঘুরছে । p বিন্দুতে বস্তুকণার গতিকে নিচের সমীকরণ আকারে লেখা যায় |
v = vₓ i + vₕ j = ( -v sinө ) i + (v cosө) j
v = ( - vyₚ/r) i + (vxₚ /r ) j
p বিন্দুতে ত্বরণ নির্ণয়ের জন্য উপরের সমীকরণ অবকল করে পাই ,
a = dv/dt = ( - v/r dyₚ/dt ) i + (v/r dxₚ/dt ) j
এখন dyₚ/dt হল গতিবেগের y উপাংশ = vₕ এবং dxₚ/dt = vₓ
অতএব, a = ( -v/r vₕ ) i + v/r vₓ )
a = ( - v²/r cosө ) i + ( - v²/r sinө ) j
ত্বরণের মান a = √ ( aₓ² + aₕ² ) = v²/r √ ( cos²ө + sin²ө ) = v²/r
⇒ a = v²/r
ত্বরণের অভিমুখ নির্ণয়ের জন্য আমাদের উপরের চিত্রের φ কোণ এর মান প্রয়োজন ।
এখন tanφ = aₕ/aₓ = ( - v²/r sinө )/ ( - v²/r cosө ) = tanө
⇒ φ = ө
অর্থাৎ ত্বরণ বৃত্তটির কেন্দ্রের দিকে ক্রিয়া করে ।
অভিকেন্দ্র ত্বরণ = v²/r = ω² r ² /r (∵ v = ω r )
অভিকেন্দ্র ত্বরণ = ω² r
বৃত্তাকার পথের বাঙ্কিং ( Banking of a Round Tracks) :
যখন কোনো গাড়ি সমতল বৃত্ত পথে বাঁক নেয় তখন উৎপন্ন অভিকেন্দ্র বল কে সামাল দেয় টায়ার ও রাস্তার সংযোগস্থলে উৎপন্ন ঘর্ষণ বল । গাড়ির ওজনের সঙ্গে লম্ব প্রতিক্রিয়া সমান হয় । ঘর্ষণ বলের পরিমাণ বেশি হলে অনেক বেশি বেগে গাড়িটি বাঁক নিতে পারবে । যদি ঘর্ষণ বল F হয় তাহলে
F = m v²/R
( যেখানে m = গাড়ির ভর , R = বক্র পথের ব্যাসার্ধ , v = বৃত্ত পথে গাড়ির বেগ )
যদি μ ঘর্ষণ গুনাঙ্ক হয় তাহলে
F ≤ μ N , N = লম্ব প্রতিক্রিয়া = mg
গাড়ির সর্বোচ্চ বেগ vₘ হলে
μ N = m vₘ²/R
⇒ μ mg = m vₘ²/R
⇒ vₘ² = μ g R
∴ vₘ = √ ( μ g R)
বক্র পথের ব্যাঙ্কিং ( Banking of curved path ) :
সমতল বৃত্ত পথে বাঁক নেওয়ার সময় ঘর্ষণ বল টায়ারের অনেক ক্ষতি করতে পারে । এই জন্য পথে ব্যাঙ্কিং অর্থাৎ রাস্তাটির বাহিরের দিকের অংশ ভিতরের দিকের অংশ থেকে সামান্য উঁচু করা হয় ।
মনেকরি একটি m ভরের গাড়ি R ব্যাসার্ধে ব্যাঙ্কিং যুক্ত বৃত্ত পথে চলছে । N₁ ও N₂ হল গাড়ির টায়ারে প্রতিক্রিয়া বল হলে মোট প্রতিক্রিয়া বল N = N₁ + N₂ গাড়ির মাঝখানে ক্রিয়া করবে । যদি ব্যাঙ্কিং কোণ θ হয় N cos θ গাড়ির ওজন mg এর সমান হবে । অনুভূমিক উপাংশ N sin θ অভিকেন্দ্র বল সরবরাহ করবে ।
সমব্যবস্থায় , N sin θ = mv²/R - F cos θ
N cos θ = mg + F sin θ
এবং F = μ N ( F = ঘর্ষণ বল , রাস্তার বাঁকের দিকে কাজ করে ) এই সমীকরণগুলো থেকে পাই।
v² = Rg ( μ + tan θ ) /( 1 - μtan θ)
⇒ tan θ = ( v² - R g μ)/( Rg + μ v² )
নিৰ্দিষ্ট v , R , μ এর জন্য উপরের সম্পর্ক থেকে ব্যাঙ্কিং কোণ জানা যাবে ।
যদি ঘর্ষণ বল শূন্য হয় তাহলে μ = ০ হবে
এবং tan θ = v² /Rg
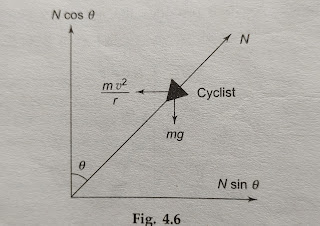
সমতল বৃত্তাকার পথে সাইকেল আরোহীর গতি ( A cyclist negotiating a curved lever road):
এক জন সাইকেল আরোহী সমতল রাস্তার ওপর বাঁক নেয় তখন অভিকেন্দ্র বল টায়ার ও রাস্তাতে উৎপন্ন ঘর্ষণ বল সাম্যবস্থা বজায় রাখে ।
অর্থাৎ m v²/R = μ N ( N = লম্ব প্রতিক্রিয়া= mg )
= μ mg
⇒ v² = μ R g
v = √ ( μ R g )
উপরের সমীকরণ থেকে আমরা বেগের সর্বোচ্চ মান পাই । এর থেকে বেশি বেগে বাঁক নিতে গেলে পিছলে পড়ে যাবে ।
যদি ঘর্ষণ বলের পরিমাণ নগন্য হয় তাহলে বাঁক নেওয়ার সময় উলম্বের সঙ্গে নিৰ্দিষ্ট কোণ করতে হবে ।
সাম্যবস্থায় আমরা পাই ,
mv²/r = N sin θ
mg = N cos θ
উপরের সমীকরণ থেকে পাই
tan θ = v²/rg
উলম্বের সঙ্গে কোণ (θ) গতিবেগ ও বক্রতা ব্যাসার্ধের ওপর নির্ভরশীল ।
উলম্ব বৃত্ত পথে বস্তুর গতি (Motion in a Vertical Circle ) :
মনে করি m ভরের একটি বস্তুকণা R ব্যাসার্ধের উলম্ব বৃত্তপথে v স্থির দ্রুতিতে ঘুরছে । শীর্ষ অবস্থান A তে সুতার টান T₁ হলে
F = T₁ + mg = mv²/R
⇒ T₁ = mv²/R - mg
অনুভূমিক বিন্দু B তে ওজনের কোনো উপাংশ কাজ করে না । যদি সুতার টান B বিন্দুতে T₂ হয় তাহলে
F = T₂ = mv²/R
C বিন্দুতে টান ও ওজন পরস্পর বিপরীত দিকে কাজ করে ।
∴ F = T₃ - mg = mv²/R
⇒ T₃ = mv²/R + mg
উপরের টানের সমীকরণ গুলি থেকে জানা যায় যে সর্বনিম্ন বিন্দু C টান সর্বোচ্চ হয় । সর্বোচ্চ বিন্দু A তে টান সর্বনিম্ন হয় । বস্তুটিকে বৃত্তাকার পথে ঘূর্ণায়মান রাখতে হলে A বিন্দুতে কমপক্ষে অভিকেন্দ্র বল বস্তুটির ওজনের সমান হবে ।
∴ mv₁²/R = mg ( v₁ = A বিন্দুতে দ্রুতি )
বেগের সর্বনিম্ন মান v₁ =√ (R g )
C বিন্দুতে সর্বনিম্ন দ্রুতি v₂ হলে ,
v₂² = v₁² + 2 x 2 R g
= Rg + 4 Rg
= 5 R g
∴ v₂ = √( 5 Rg)
C বিন্দুতে সর্বনিম্ন টান হবে T₃ = m v₂² /R + mg
= 5 mg + mg
⇒ T₃ = 6mg
জলভর্তি একটি বালতি কে উলম্ব বৃত্তাকার পথে ঘোরানো হচ্ছে । যদি অভিকেন্দ্র বল mv²/R ওজনের থেকে বেশি হয় তাহলে জল পড়বে না । আর যদি mg > mv²/R হয় তাহলে কিছু পরিমাণ জল পড়ে যাবে । বাকি জলের ওজন ও অভিকেন্দ্র বল পরস্পর সমান থাকে ।
বহু বিকল্প ভিত্তিক প্রশ্ন (MCQ) : ( https://forms.gle/eZHT3rYWCgvATUMt5 )
1. একটি প্রাসের সর্বোচ্চ উচ্চতা ও অনুভূমিক পাল্লা সমান হলে এবং অনুভূমিকের সঙ্গে θ কোণ করলে নিচের কোনটি সত্য ?
a) θ = tan⁻¹ 2 b) θ = tan⁻¹ 3
c) θ = tan⁻¹4 d) θ = tan⁻¹ 5
2. 100 m অনুভূমিক দুরত্বে অবস্থিত একটি বস্তুকে এক ব্যক্তি তাঁর বন্দুক দিয়ে তাক করলেন । বন্দুক থেকে গুলি 500 m/s অনুভূমিক বেগ নিয়ে বের হয় । ওই ব্যক্তি লক্ষ্য বস্তুর কত উপরে লক্ষ্য স্থির করবেন ? ( g = 10 m s⁻² )
a) 10 cm b) 20 cm
c) 50 cm d) 100 cm
3.প্রাসের সর্বোচ্চ বিন্দুতে গতিবেগ ও ত্বরণের অভিমুখ কোনটি হবে ?
a) পরস্পর সমান্তরাল হবে । b) পরস্পর বিপরীত সমান্তরাল (anti parallel) হবে ।
c ) পরস্পর 45º কোণে নত থাকবে । d) পরস্পরের উপর লম্ব হবে ।
4. 19.6 m উঁচু একটি বাড়ির ছাদ থেকে একটি বলকে 5 m/ s বেগে অনুভূমিক দিকে ছোঁড়া হল । বলটি কত সময় পরে মাটিতে পড়বে ?
a) √2 s b) 2 s
c) √3 s d) 3 s
5 . লক্ষ্য বস্তুর ঠিক h উচ্চতায় একটি বিমান থেকে একটি বোমা নিক্ষেপ করা হলো । বোমাটি কত দুরত্বে লক্ষ্য বস্তুকে মিস ( miss ) করবে ? বিমানটির অনুভূমিক দিকে গতিবেগ v |
a) 2v √(h/g) b) v √(h/g)
c) v √(2h/g) d) v √(h/2g)
6. শত্রু পক্ষের দেশে 100 km দুরত্ব থেকে তোমার শহরে একটি Missile সর্বোচ্চ পাল্লাতে ছোঁড়া হল । Missile টি যদি অর্ধ দুরত্বে আবিষ্কৃত হয় তাহলে সতর্কীকরণের জন্য কত সময় পাওয়া যাবে ?( g = 10 m/s² )
a) 100 s b) 100/√2 s
c) 100 √(3/2) s d) 200 s
7. 6 নম্বর প্রশ্নে মিসাইল টি যখন আবিষ্কৃত হয় তখন তার দ্রুতি কত ছিল ?
a) 200 √2 m s⁻¹ b) 300 √2 m s⁻¹
c) 400 √2 m s⁻¹ d) 500 √2 m s⁻¹
8 . 6 নম্বর প্রশ্নে মিসাইল টির সর্বোচ্চ উচ্চতা কত ?
a) 2.5 x 10⁴ m b) 5.0 x 10⁴ m
c) 7.5 x 10⁴ m d) 10⁵ m
9. 6 নম্বর প্রশ্নে মিসাইল টি কত বেগে মাটিতে লক্ষ্য বস্তুকে আঘাত করবে ?
a) 10² m s⁻¹ b) 10³ m s⁻¹
c) 10⁴ m s⁻¹ d) 10⁵ m s⁻¹
10. একটি বিমান v ms⁻¹ সম দ্রুতিতে উড়ছে । t সেকেন্ড সময়ের ব্যবধানে বিমানটির দুটি অবস্থানের জন্য ভূমিতে কোনো লক্ষ্য বস্তুতে θ কোণ উৎপন্ন করে । বিমানটি ভূমি থেকে কত উচ্চতায় উড়ছে ?
a) vt /(2 tan θ) b) 2vt /tanθ
c) vt /tan( θ/2) d) vt / [2tan(θ/2)]
11. শত্রু পক্ষের একটি বিমান মাটি থেকে 2 km উচ্চতায় 300 ms⁻¹ বেগে উড়ছে । মাটিতে একজন সৈন্য ঠিক তার মাথার উপরে বিমানটিকে দেখতে পেল এবং সে তার বন্দুক থেকে 600 ms⁻¹ বেগে গুলি ছুঁড়লো । উলম্বের সঙ্গে কত কোণে গুলি ছুঁড়লে বিমানটিকে ঠিক আঘাত করবে ?
a) 30º b) 45º
c) 60º d) 75º
12. 11 নম্বর প্রশ্নে বিমানটি সর্বনিম্ন কত উচ্চতায় উড়লে গুলির আঘাত থেকে রক্ষা পাবে ?
a) 12.5 km b) 13.5 km
c) 14.5 km d) 15.5 km
13.একজন ক্রিকেটার অনুভূমিক দিকে সর্বোচ্চ 100 m পর্যন্ত বল ছুঁড়তে পারে । যদি ওই একই প্রচেষ্টায় উলম্ব দিকে বল ছুঁড়ে তাহলে সর্বোচ্চ কত উচ্চতায় ছুঁড়তে পারবে ?
a) 50 m b) 60 m
c) 70 m d) 80 m
14 . 40 m উঁচু একটি স্থম্ভের শীর্ষদেশ থেকে 20 m /s বেগে এবং 30º উন্নতি কোণে একটি বল ছোঁড়া হলো । মাটিতে পৌঁছাতে মোট সময় ও উড্ডয়ন কালের ( যে উচ্চতা থেকে ছোঁড়া হয়েছিল সেই উচ্চতায় পৌঁছাতে সময় ) অনুপাত কত ? ( g = 10 m /s² )
a) 2 : 1 b) 3 : 1
c) 3 : 2 d) 1.5 : 1
15 . 14 নম্বর প্রশ্নে স্তম্ভের পাদদেশ থেকে কত দূরত্বে বলটি ভূমি স্পর্শ করবে ?
a) 50 m b) 60 m
c) 70 m d) 80 m
16. R দুরত্বে অবস্থিত একটি উলম্ব দেয়ালকে লক্ষ্য করে একটি কামান থেকে v₀ বেগে অনুভূমিকের সঙ্গে α কোণ করে গোলা ছোঁড়া হল । গোলটি ভূমি থেকে কত উচ্চতায় দেয়ালটিকে স্পর্শ করবে ?
a) R sin α - 1/2 gR² /(v₀² sin²α) b) R cos α - 1/2 gR² /(v₀² cos²α)
c) R tanα - 1/2 gR² /(v₀² cos²α) d) R tan α - 1/2 gR² /(v₀² sin²α)
17. r দূরত্বে অবস্থিত একটি বিন্দু P কে অতিক্রম করার জন্য দুটি বিভিন্ন কোণে কোনো বস্তুকে ছোঁড়া যায় । P বিন্দুতে পৌঁছানোর দুইটি সময়ের গুনফল নিচের কোনটির সমানুপাতিক ?
a) 1/r b) r
c) r³ d) 1/r²
18. একটি প্রাসের সর্বোচ্চ পাল্লা 200 m | বস্তুটি সর্বোচ্চ কত উচ্চতায় উঠেবে ?
a) 25 m b) 50 m
c) 75 m d) 100 m
19. 30⁰ নতিতে অবস্থিত একটি ঘর্ষণহীন নততল বরাবর একটি বস্তু 40 মিটার পতিত হয়ে একটি বেগ লাভ করে । ওই একই বেগে বস্তুটি অনুভূমিকের সঙ্গে 30⁰ কোণ করে ছোড়লে এর পাল্লা কত হবে / ( g = 10 m/s² )
a) 20 m b) 20 √2 m
c) 20 √3 m d) 40 m
20 .একটি গ্রহ থেকে নিক্ষিপ্ত প্রাসের গতির ক্ষেত্রে নিচের কোনটি ধ্রুবক থাকে ?
a) গতিশক্তি b) ভরবেগ
c) গতিবেগের উলম্ব উপাংশ d) গতিবেগের অনুভূমিক উপাংশ
[ উপরের MCQ গুলির উত্তর জানতে হলে নিচের লিংকটিতে ক্লিক বা কপি করে google এ paste করো এবং সঠিক উত্তরটি টিক দিয়ে submit করো । https://forms.gle/eZHT3rYWCgvATUMt5 ]










কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন