আলো (Light)
গোলীয় দর্পনে আলোর প্রতিফলন (Reflection at Spherical Mirror):
সমতল দর্পনে সমান্তরাল আলোক রশ্মি গুচ্ছ আপতিত হলে সমান্তরাল আলোক রশ্মি গুচ্ছ হিসাবেই প্রতিফলিতা হয় । কিন্তু গোলীয় দর্পনে সমান্তরাল আলোকরশ্মি গুচ্ছ প্রতিফলিত হলে অভিসারী বা অপসারী আলোকরশ্মি গুচ্ছে পরিণত হয় । যে দর্পন কোনো গোলকের তলের অংশ বিশেষ হয় তাকে গোলীয় দর্পন বলে ।
গোলীয় দর্পন দুই প্রকারের হয় - 1) অবতল দর্পন(Concave Mirror) 2) উত্তল দর্পন (Convex Mirror)

অবতল দর্পন (Concave Mirror) :
যে গোলীয় দর্পনের অবতল পৃষ্ট প্রতিফলক হিসাবে বাবহৃত হয় তাকে অবতল দর্পন বলে ।
উত্তল দর্পন ( Convex Mirror) :
যে গোলীয় দর্পনের উত্তল পৃষ্টে আলোর প্রতিফলন ঘটে তাকে উত্তল দর্পন বলে ।
গোলীয় দর্পনের বক্রতা কেন্দ্র , বক্রতা ব্যাসার্ধ , মেরু ও প্রধান অক্ষ ,ফোকাস দর্ঘ্য :
বক্রতাকেন্দ্র ( Centre of Curvature) :
কোনো গোলীয় দর্পন যে গোলকের অংশ সেই গোলকের কেন্দ্রকে ওই দর্পনের বক্রতা কেন্দ্র বলে ।
বক্রতাব্যাসার্ধ (Radius of Curvature) :
গোলীয় দর্পন যে গোলকের অংশ তার ব্যাসার্ধকেই ওই গোলীয় দর্পনের বক্রতা ব্যাসার্ধ বলে ।
মেরু (Pole) :
কোনো গোলীয় দর্পনের মধ্য বিন্দুকে দার্পনটির মেরু বলে ।
প্রধান অক্ষ ( Principal Axis):
গোলীয় দর্পনের বক্রতা কেন্দ্র ও মেরুর সংযোজক সরলরেখাকে প্রধান অক্ষ বলে ।
ফোকাস দৈঘ্র্য ( Focal Length):
মেরু এবং মুখ্য ফোকাসের মধ্যবর্তী দূরত্বকে ফোকাস দৈর্ঘ্য বলে ।
মুখ্যফোকাস (Principal Focus):
প্রধান অক্ষের সমান্তরাল এক গুচ্ছ সমান্তরাল আলোকরশ্মি অবতল দর্পনে প্রতিফলিত হয়ে প্রধান অক্ষের উপর যে বিন্দুতে মিলিত হয় সেই বিন্দুকে অবতল দর্পনের মুখ্য ফোকাস বলে ।

অনুরূপ ভাবে বলা যায় প্রধান অক্ষের সমান্তরাল আলোকরশ্মি গুচ্ছ উত্তল দর্পনে প্রতিফলিত হয়ে প্রধান অক্ষের যে বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয় সেই বিন্দুটিকে উত্তল দর্পনটির মুখ্য ফোকাস বলে ।

উপাক্ষিয় রশ্মির ধারণা ও ঊপাখিয় রশ্মির ক্ষেত্রে r = 2f প্রদর্শন :


দর্পনের প্রধান অক্ষের নিকটবর্তী আপতিত আলোকরশ্মিকে বলা হয় উপক্ষিয়(Paraxial Rays) রশ্মি । একটি প্রধান অক্ষের সমান্তরাল উপাখিয় রশ্মি AB প্রতিফলনের পর মুখ্য ফোকাস F এর মধ্য দিয়ে যাবে ।B বিন্দুতে দর্পনের উপর অঙ্কিত লম্ব BC বক্রতা কেন্দ্র C বিন্দু দিয়ে যাবে । চিত্র থেকে পাই - আপতন কোন < ABC = i এবং প্রতিফলন কোন <CBF = r .
প্রতিফলনের সুত্রানুযায়ী , ∠ ABC = ∠ CBF এবং ∠ ABC = ∠ BCF = θ (একান্তর কোন )
∴ r = θ অর্থাৎ ΔABC একটি সমবাহু ত্রিভুজ যার BF = CF | উপক্ষিয় রশ্মির ক্ষেত্রে B এবং P খুব নিকটবর্তী হওয়ায় PF = BF অর্থাৎ F হলো CP এর মধ্য বিন্দু ।
∴ PF = f = 1/2 CP = 1/2 r ( BC = CP =r)
ஃ r = 2f
গোলীয় দর্পনে আলোর প্রতিফলনের জন্য প্রতিবিম্ব গঠন :
গোলীয় দর্পনে প্রতিবিম্ব গঠনের নিয়ম : 1 )প্রধান অক্ষের সমান্তরাল আলোক রশ্মি প্রতিফলনের পর মুখ্য ফোকাস দিয়ে যায় । 2) কোনো আপতিত আলোকরশ্মি মুখ্য ফোকাস দিয়ে গিয়ে প্রতিফলনের পর প্রধান অক্ষের সমান্তরাল হয়ে যায় । 3) বক্রতা কেন্দ্রের মধ্য দিয়ে গমনশীল আলোক রশ্মি লম্ব ভাবে দর্পনে আপতিত হয় , ফলে প্রতিফলনের পর একই পথে বিপরীত দিকে ফিরে যায় । উপরের তিনটি নিয়মের যেকোনো দুটির সাহায্যে আমরা প্রতিবিম্ব গঠন করতে পারি ।

অবতল দর্পনে প্রতিবিম্ব গঠনের নিয়ম :
প্রধান অক্ষের সমান্তরাল আলোকরশ্মি AD প্রতিফলিত হয়ে ফোকাস F এর মধ্য দিয়ে গমন করে । A বিন্দু আগত আর একটি আলোক রশ্মি AE বক্রতা কেন্দ্র C দিয়ে গমন করে প্রতিফলিত হয়ে ওই একই পথে বিপরীত দিকে অগ্রসর হয় । এই দুই আলোকরশ্মি প্রতিফলনের পরে A ' বিন্দুতে মিলিত হয় । A' বিন্দুই হল A বিন্দুর সৎবিম্ব ।
অবতল দর্পনে যদি বস্তু ফোকাস দূরত্বের বাইরে থাকে তাহলে বস্তুর একটি সৎবিম্ব গঠিত হয় । আর যদি বস্তু ফোকাস দূরত্বের মধ্যে অবস্থান করে তাহলে বস্তুটির একটি অসৎবিম্ব গঠিত হয় ।
উত্তল দর্পনে প্রতিবিম্ব গঠন :

উত্তল দর্পনে সবসময় খর্বাকৃতি অসৎপ্রতিবিম্ব গঠিত হয় ।
আলোর প্রতিসরণ ( Refraction of Light) :
আলোকরশ্মি যখন এক সমসত্ত্ব সচ্ছ মাধ্যম থেকে অন্য একটি সচ্ছ সমসত্ম মাধ্যমে তীর্যক ভাবে প্রবেশ করে তখন দুই মাধ্যমের বিভেদতলে আলোকরশ্মি অভিমুখ পরিবর্তন করে । এই ঘটনাকে আলোকের প্রতিসরণ বলে ।

প্রতিসরণের সূত্রাবলি ( laws of Refraction):
প্রথম সূত্র : আপতিত রশ্মি , প্রতিসৃত রশ্মি ও আপতন বিন্দুতে দুই মাধ্যমের বিভেদ তলের উপর অঙ্কিত অভিলম্ব একই সমতলে থাকে ।
দ্বিতীয় সূত্র : দুটি নিৰ্দিষ্ট মাধ্যমের বিভেদতলে একটি নিৰ্দিষ্ট বর্ণের আলোর প্রতিসরণ হলে আপতন কোনের সাইন ও প্রতিসরণ কোনের সাইন এর অনুপাত সর্বদা ধ্রুবক থাকে ।

দ্বিতীয় সূত্র অনুসারে পাই ,
sin θi / sin θr = n₁/n₂ = ধ্রুবক = ₁n₂; n₁ হল প্রথম মাধ্যমের পরম প্রতিসরাঙ্ক n₂ হল দ্বিতীয় মাধ্যমের পরম প্রতিসরাঙ্ক ।₁n₂ হল প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের প্রতিসরাঙ্ক ।উপরের সূত্রটিকে স্নেলের সূত্র বলে ।
প্রতিসরণের ফলে আলোকরশ্মির চ্যুতি :
প্রতিসরণের সময় আলোকরশ্মি যে কোনে বেঁকে যায় তাকে চ্যুতি বলে ।
লঘু থেকে ঘন মাধ্যমে প্রতিসরণের সময় চ্যুতি :
স্নেলের সূত্র থেকে পাই n2 > n1
অর্থাৎ sin θi / sin θr > 1 ⇒sin θi > sin θr
∴ θi > θr হয় ।
প্রতিসৃত রশ্মিটি অভিলম্বের দিকে সরে যায় । এক্ষেত্রে চ্যুতি হয় (θi - θr) ।
 চিত্রে চ্যুতি d = i - r
চিত্রে চ্যুতি d = i - r
ঘন মাধ্যম থেকে লঘু মাধ্যামে প্রতিসরণের সময় চ্যুতি :

এক্ষেত্রে চ্যুতি d = r - i
প্রিজম (Prism):
তিনটি আয়তাকার তল ও দুটি ত্রিভুজাকার তল দ্বারা সীমাবদ্ধ সচ্ছ প্রতিসারক মাধ্যমকে প্রিজম বলে ।
প্রতিসরাক তল :
যে আয়তাকার তলগুলিতে আলো আপতিত হলে আলোর প্রতিসরণ হয় সেই তলগুলিকে প্রতিসারক তল বলে । প্রিজমে আয়তাকার তলগুলি প্রতিসারক হয় ।
প্রতিসারক কোন :
দুটি প্রতিসারক তল মিলিত হয়ে কোণ উৎপন্ন হয় তাকে পপ্রিজমের প্রতিসারক কোন বলে ।

প্রান্ত রেখা :
প্রিজমের দুটি প্রতিসারক তল যে রেখায় মিলিত হয় তাকে প্রান্ত রেখা বলে ।
ভূমি :
প্রিজমের যে কোনো প্রান্তরেখার বিপরীত তলকে ভূমি বলে ।
প্রধান ছেদ : যে তল প্রিজমের প্রতিসারক তলকে লম্ব ভাবে ছেদ করে তাকে প্রাধান ছেদ বলে ।
প্রিজমের মধ্য দিয়ে প্রতিসৃত রশ্মির চ্যুতি কোন :

ধরা যাক ABC হল প্রিজমের একটি প্রধান ছেদ । A হল প্রিজম কোন ।প্রিজমটির উপাদানের প্রতিসরাঙ্ক μ ।
AB প্রতিসরাক তলে আপতিত রশ্মির আপতন কোন i1 এবং প্রতিসরণ কোন r1 |অনুরূপভাবে AC প্রতিসরাক তলে আপতন কোন r2 এবং প্রতিসরণ কোন ( নির্গমন কোন) i2 | আপতিত ও নির্গমন রশ্মির মধ্যে চ্যুতি কোন∠ LMQ = δ । চিত্র থেকে পাই ∠ MPQ = (i1 - r1 ) এবং ∠MQP = (i2 -r2 ) |
ஃ চ্যুতি কোন δ = ∠ MPQ + ∠MQP = (i1 - r1 ) +(i2 -r2 ) = (i1 + i2 ) -(r1 +r2)
APNQ চতুর্ভূজ থেকে পাওয়া যায়
∠A + ∠N = 180 ডিগ্রী ।( ∠APN = ∠ AQN = 90 ডিগ্রী ।)
আবার PQN ত্রিভুজ থেকে পাই ∠ N + r1 +r2 = 180 ডিগ্রী ।
⇒ r1 +r2 = A
ஃ δ = i₁ +i₂-(r₁ +r₂) = i₁ +i₂ - A
⇒ δ = i₁ +i₂ - A
কাঁচের স্ল্যাবের মধ্য দিয়ে আলোর প্রতিসরণ :
সমান্তরাল পৃষ্ঠযুক্ত একটি কাঁচের ফলকের মধ্য দিয়ে আলোর প্রতিসরণের সময় আলোকরশ্মির কোনো কৌণিক চ্যুতি হয় না ।

উপরের চিত্রে AB আপতিত রশ্মি BC প্রতিসৃত রশ্মি C বিন্দুতে পুনরায় প্রতিসৃত হয়ে CD পথে বহির্গত হয় ।
A বিন্দুতে প্রতিসরণের বেলাই লেখা যায় ,
Sini₁ /Sinr₁= μ ( μ কাঁচের প্রতিসরাঙ্ক ) অনুরূপে C বিন্দুতে প্রতিসরণের ক্ষেত্রে লেখা যায় ,
Sin i₂/ Sinr₂ = 1/μ
এখানে r₁ = i₂ ( B ও C বিন্দুতে অভিলম্ব দুইটি সমান্তরাল ।)
∴ sini₁ /sinr₁ = Sinr₂ / Sini₂
⇒ Sin i₁ = Sinr₂
∴ i₁ = r₂ আপতিত রশ্মি ও নির্গত রশ্মি পরস্পর সমান্তরাল ।
লেন্স (Lens):
দুটি গোলীয় তল বা একটি গোলীয় ও একটি সমতল দ্বারা সীমাবদ্ধ সচ্ছ প্রতিসরাক মাধ্যমকে লেন্স বলে ।
লেন্স প্রধানত দুই প্রকারের হয় । উত্তল লেন্স ও অবতল লেন্স ।
উত্তল লেন্স (Convex lens):
যে লেন্সের মধ্যভাগ মোটা ও প্রান্তের দুই দিক ক্রমশ সরু সেই লেন্সকে উত্তল লেন্স বা অভিসারী লেন্স বলে ।
অবতল লেন্স (Concave lens) :
যে লেন্সের মধ্য ভাগ সরু প্রান্তের দুই ক্রমশ মোটা তাকে অপসারী বা অবতল লেন্স বলে ।

লেন্স সম্পর্কিত কয়কেটি সংজ্ঞা (Some definitions about lens):
বক্রতা কেন্দ্র ( Centre of Curvature) : লেন্সের কোনো গোলীয় তল যে গোলকের অংশ সেই গোলকের কেন্দ্রকে ওই প্রতিসরাক তলের বক্রতা কেন্দ্র বলে ।দুটি গোলীয় তল বিশিষ্ট লেন্সের দুটি বক্রতা কেন্দ্র থাকে ।
বক্রতা ব্যাসার্ধ (Radius of Curvature):
লেন্সের কোনো গোলীয় তল যে গোলকের অংশ সেই গোলকের ব্যাসার্ধকে ওই তলের বক্রতা ব্যাসার্ধ বলে ।
প্রধান অক্ষ (Principal axis):
লেন্সের দুটি বক্রতা কেন্দ্রের সংযোজক সরলরেখাকে লেন্সটির প্রধান অক্ষ বলে ।
উন্মেষ (Aperture): লেন্সের ব্যাসকে উন্মেষ বলে ।

সরু বা পাতলা লেন্স (Thin lens):
লেন্সের প্রধান অক্ষ লেন্সটির দুটি গোলীয় তলকে যে দুটি বিন্দুতে ছেদ করে সেই দুটি বিন্দুর দুরত্ব কে ওই লেন্সের বেধ (Thickness ) বলে । যে লেন্সের বেধ তার বক্রতা ব্যাসার্ধ অপেক্ষা খুব ছোটো সেই লেন্সকে পাতলা লেন্স বলে ।
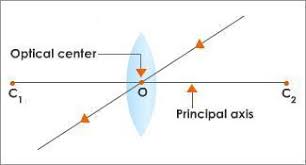
আলোককেন্দ্র (Optical centre):
আলোককেন্দ্র হল লেন্সের অভ্যন্তরে প্রধানক্ষের উপরে এমন একটি বিন্দু যে বিন্দুর মধ্যে দিয়ে কোনো আলোকরশ্মি গমন করলে ওর কোনো অভিমুখের পরিবর্তন হয় না । অর্থাৎ নির্গত রশ্মি আপতিত রশ্মির সমান্তরাল হয় ।

ফোকাস ,ফোকাস দূরত্ব (Focus, Focul length):
উত্তল লেন্সের ক্ষেত্রে প্রধান অক্ষের সমান্তরাল আলোকরশ্মি গুচ্ছ লেন্সের দ্বারা প্রতিসৃত হয়ে প্রাধান অক্ষের উপর যে বিন্দুতে মিলিত হয় অথবা অবতল লেন্সের ক্ষেত্রে যে বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয় ,সেই বিন্দুকে লেন্সটির প্রধান বা মুখ্য ফোকাস বলে ।।

লেন্সের আলোককেন্দ্র থেকে প্রধান ফোকাস পর্যন্ত দূরত্বকে ফোকাস দুরত্ব বলে । একে f চিহ্ন দ্বারা প্রকাশ করা হয় ।
উত্তল লেন্সকে অভিসারী লেন্স বলা হয় কারণ প্রধান অক্ষের সমান্তরাল আলোকরশ্মি উত্তল কর্তৃক প্রতিসৃত হয়ে অভিসারী আলোকরশ্মি গুছে পরিণত হয় ।অন্যদিকে অবতল লেন্সকে অপসারী লেন্স বলে কারণ এতে প্রধান অক্ষের সমান্তরাল রশ্মিগুচ্ছ প্রতিসৃত হয়ে অপসারী অলোকরশ্মি গুচ্ছে পরিণত হয় ।
উত্তল লেন্স দ্বারা প্রতিবিম্ব গঠন (Formation of image by convex lens):
উত্তল লেন্সের ক্ষেত্রে প্রতিবিম্ব গঠনের সময় নিম্নলিখিত ধর্মগুলি কাজে লাগানো হয় -
1) প্রধান অক্ষের উপর লম্বভাবে অবস্থিত বস্তুর প্রতিবিম্বও প্রধান অক্ষের উপর লম্ব হয় ।
2) যে রশ্মি গুলি প্রধান অক্ষের প্রধান অক্ষের সমান্তরাল ভাবে আপতিত হয় সেই রশ্মিগুলি প্রতিসরণের পর প্রধান ফোকাস দিয়ে গমন করে ।
3) যে রশ্মিগুলি আলোককেন্দ্র দিয়ে যায় সেগুলির কোনো অভিমুখের পরিবর্তন হয় না ।
রশ্মিচিত্র গঠন (Construction of ray diagram) :
1. বস্তু যখন অসীম দূরত্বে অবস্থিত :
বস্তু অসীম দূরত্বে থাকলে প্রতিবিম্ব ফোকাস তলে গঠিত হয় । প্রতিবিম্ব সৎ, উল্টানো ও আকারে খুব ছোটো হয় ।

2.বস্তু লেন্স থেকে 2f অপেক্ষা বেশি দূরে অবস্থিত :
এক্ষেত্রে প্রতিবিম্ব সৎ ,উল্টানো এবং বস্তুর চেয়ে আকারে ছোট হয় ।

AB বস্তুর প্রতিবিম্ব A¹B¹ |
3. বস্তু লেন্স থেকে 2f দূরত্বে অবস্থিত :
এক্ষেত্রে প্রতিবিম্ব সৎ , উল্টানো এবং বস্তুর সমান আকৃতির হয় ।
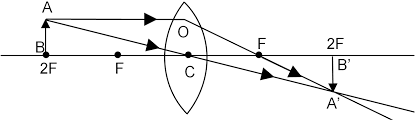
4. বস্তু f এবং 2f দূরত্বের মধ্যে অবস্থিত :
এক্ষেত্রে সৎ ,উল্টানো ও বস্তুর চেয়ে বড় আকৃতির প্রতিবিম্ব গঠিত হয় ।

5. বস্তু লেন্সের ফোকাসে অবস্থিত :
এখানে প্রতিবিম্বটি অসীমে তৈরি হয় এবং বিশাল আকৃতির সৎ বিম্ব হয় ।

6. বস্তু লেন্সটির ফোকাসের মধ্যে অবস্থিত :
বস্তুকে আলোককেন্দ্র ও ফোকাসের মধ্যে রাখলে বস্তুটি লেন্সটির যেদিকে আছে সেই দিকেই একটি বিবর্ধিত অসৎ সমশীর্ষ প্রতিবিম্ব গঠিত হয় ।

অবতল লেন্সের দ্বারা প্রতিবিম্ব গঠন :
এক্ষেত্রে বস্তুর সবসময় অসৎ সমশীর্ষ ও খর্বাকৃতি প্রতিবিম্ব গঠিত হয় ।

ৰৈখিক বিবর্ধন (Linear magnification) :
প্রতিবিম্ব ও বস্তুর দৈঘ্যের অনুপাতকে ৰৈখিক বিবর্ধন বলে । প্রমান করা যায় যে ৰৈখিক বিবর্ধন প্রতিবিম্ব এর দূরত্ব ও বস্তু দূরত্বের অনুপাতের সমান ।

বিবর্ধক কাচ (Magnifying glass):
এটি হল কম ফোকাস দৈঘ্যের একটি উত্তল লেন্স ।উত্তল লেন্সের ফোকাসের মধ্যে বস্তু ধরলে বস্তুটির একটি বিবর্ধিত অসৎ প্রিতবিম্ব গঠিত হয় ।

মানুষের চোখের দৃষ্টি সমস্যা :
স্বাবাবিক চোখ 25 সেমি থেকে অসীম দূরত্ব পর্যন্ত দেখতে পায় । একে বলা হয় স্বাবাবিক চোখের দৃষ্টির পাল্লা । ত্রুটি পূর্ণ চোখের দৃষ্টির পাল্লা স্বাভাবিক চোখের তুলনায় কম হয় । মানুষের চোখের সাধারণত দুই প্রকারের ত্রুটি দেখা যায় । ১. দীর্ঘ দৃষ্টি ২. স্বল্প দৃষ্টি
1.দীর্ঘ দৃষ্টি (Hypermetropia):
এই ক্ষেত্রে চোখ দূরের জিনিস স্পষ্ট দেখতে পায় ,কিন্ত কাছের জিনিস স্পষ্টভাবে দেখতে পায় না । এক্ষেত্রে স্পষ্ট দর্শনের ন্যূনতম দুরত্ব 25 সেমি অপেক্ষা বেশি হয় । অক্ষিগোলকের আকার ছোটো হলে বা অক্ষি লেন্সের ফোকাস দৈঘ্য বেড়ে গেলে এই রকম ত্রুটি দেখা যায় । ফলে প্রতিবিম্ব রেটিনা তে তৈরি না হয়ে রেটিনার পেছনে তৈরি হয় । এই ত্রুটি দূর করার জন্য উত্তল লেন্সের চশমা ব্যবহার করা হয় । চশমার পাওয়ার পজিটিভ হয় ।

স্বল্প দৃষ্টি (Myopia):
এক্ষেত্রে চোখ কাছের জিনিস স্পষ্ট দেখতে পায় কিন্তু দূরের জিনিস ভালো দেখতে পায় না । দূরের বস্তু থেকে আগত রশ্মিগুচ্ছ চোখের লেন্স দ্বারা প্রতিসৃত হয়ে রেটিনার সামনের বিন্দুতে মিলিত হয় । চোখের লেন্সের ফোকাস দূরত্ব কমে গেলে এই ধরনের ত্রুটি দেখা যায় । এটি প্রতিকারের জন্য অবতল লেন্সের চশমা ব্যবহার করতে হয় ।
চশমার পাওয়ার নেগেটিভ হয় ।

আলোর বিচ্ছুরণ (Dispersion of Light):
যৌগিক আলো কোনো সচ্ছ মাধ্যম যেমন প্রিজমের মধ্যে গিয়ে বিভিন্ন বর্ণে বিভক্ত হওয়ার ঘটনাকে আলোর বিচ্ছুরণ বলে ।
প্রিজমের সাহায্যে সাদা আলোর বিচ্ছুরণ ( Dispersion of white light by prism) :
সাদা আলো প্রিজমের মধ্যে প্রতিসৃত হয়ে সাতটি বিভিন্ন বর্ণের আলোকে বিশ্লিষ্ট হয়ে যায় । এই সাতটি বিভিন্ন বর্ণের যে আলোর পটি পাওয়া যায় তাকে বর্ণালী বলে ।
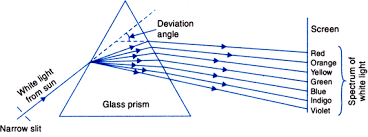
একটি সাদা আলোকরশ্মি প্রিজমটির প্রথম প্রতিসারক তলে আপতিত হলে ওই রশ্মি থেকে সাতটি আলাদা আলাদা বর্ণের আলোক রশ্মি পাওয়া যায় । বিভিন্ন বর্ণের আলোর প্রতিসরাঙ্ক তথা গতিবেগ বিভিন্ন হওয়ায় বর্ণগুলি পাওয়া যায় । বিভিন্ন বর্ণগুলির চ্যুতিও বিভিন্ন হয় । দ্বিতীয় প্রতিসরাক তল থেকে আরো অধিক বিচ্যুতি নিয়ে বাইরে বেরিয়ে আসে । এখানে দুই প্রতিসরাক তলে বিভিন্ন বর্ণগুলির বিচ্যুতি একই অভিমুখে হয় ফলে বর্ণালী পাওয়া যায় । বিভিন্ন যৌগিক বর্ণগুলি হল বেগুনী ,নীল ,আকাশীনীল ,সবুজ ,হলুদ ,কমলা ও লাল । মনে রাখার জন্য সমস্ত বর্ণগুলির আদ্যাক্ষর নিয়ে একটি শব্দ গঠন করা যায় । শব্দটি হল -বেনীআসহকলা । ইংরেজিতে শব্দটি - VIBGYOR ।
আয়তাকার কাচের স্ল্যাবের মধ্যেদিয়ে সাদা আলো প্রতিসৃত হলে বর্ণালী পাওয়া যায় না কারণ এখানে দুই বিপরীত প্রতিসারক তলে বিভিন্ন বর্ণের আলোগুলির বিচ্যুতি পরস্পর বিপরীত দিকে ঘটে । ফলে মোট বিচ্যুতি শূন্য হয় ।
একবর্ণী আলো (Monochromatic light):
সাদা আলো হল এক প্রকারের যৌগিক আলো ,কারণ সাদা আলো সাতটি বিভিন্ন বর্ণের আলোর সমষ্টি । এই এক একটি বর্ণ হল একবর্ণী আলো । কোনো অসচ্ছ বস্তুর বর্ণ নির্ভর করে বস্তুটি কোন বর্ণের আলো প্রতিফলন করতে পারে তার ওপর । লাল রঙের বস্তুর উপর সাদা আলো পড়লে কেবল লাল রংটি প্রতিফলিত হয় অন্য বর্ণের আলোগুলি শোষিত হয় ।তাই বস্তুটির রঙ লাল হয় । লাল বর্ণের জবা ফুলের উপর নীল আলো পড়লে ফুলটিকে কালো দেখাবে ।
কারণ লাল ফুল নীল রঙ কে শোষণ করে নিবে । জবা ফুল থেকে কোনো বর্ণের আলো প্রতিফলিত হবে না । সুতরাং ফুলটিকে কালো দেখাবে কারণ কালো রঙ হলো সমস্ত রঙের অনুপস্থিতি ।কোনো সচ্ছ বস্তুর বর্ণ নির্ভর করে বস্তুর মধ্য দিয়ে নির্গত আলোর বর্ণের ওপর । নীলবর্ণের কাচের উপর সাদা আলো পড়লে শুধু নীলবর্ণটি কাচের ভিতর দিয়ে নির্গত হবে । অন্য্ বর্ণগুলি শোষিত হবে । ফলে কাচটি নীল দেখাবে ।
আলোকতরঙ্গ ( Light wave) :
আলো এক প্রকারের তড়িৎচুম্বকীয় তির্যক তরঙ্গ ( electromagnetic wave) | এই তরঙ্গ বিস্তারের জন্য কোনো জড় মাধ্যমের প্রয়োজন হয় না ।
তরঙ্গ সম্পর্কিত কয়টি সংজ্ঞা :
কম্পাঙ্ক (Frequency) :
এক সেকেন্ডে কোনো মাধ্যমের মধ্যে যতগুলি পূর্ণ তরঙ্গের সৃষ্টি হয় তাকে তরঙ্গের কম্পাঙ্ক বলে । কম্পাঙ্কের SI একক হলো হার্ৎজ (Hz) |

তরঙ্গদৈর্ঘ্য (Wave length) :
কোনো তরঙ্গের উপরিস্থিত সমদশা সম্পন্ন পরপর দুটি বিন্দুর দূরত্ত্বকে ওই তরঙ্গের তরঙ্গ দৈর্ঘ্য বলে । তরঙ্গদৈর্ঘ্য এর SI একক মিটার ।

তরঙ্গবেগ (Wave velocity):
একক সময়ে কোনো তরঙ্গ যে দূরত্ব অতিক্রম করে তাকে তরঙ্গবেগ বলে । এর SI একক m/s | শূন্য মাধ্যমে সব বর্ণের আলো একই বেগে গমন করে । এই বেগের মান 3 x 10⁸ m/s | কিন্তূ কোনো মাধ্যমে আলোর বেগ উহার তরঙ্গদৈর্ঘ্যের ওপর নির্ভর করে । আলোর তরঙ্গ তত্ত্ব অনুসারে কোনো মাধ্যমের প্রতিসরাঙ্ক শুন্যমাধ্যমে আলোর বেগ ও ওই মাধ্যমে আলোর বেগের অনুপাতের সমান ( μ = c/v ) | বিভিন্ন বর্ণের প্রতিসরাঙ্ক বিভিন্ন হওয়ায় বিভিন্ন বর্ণের আলোর গতিবেগও বিভিন্ন হয় ।লাল বর্ণের গতিবেগ সবচেয়ে বেশি হয় এবং বেগুনি বর্ণের গতিবেগ সবচেয়ে কম হয় ।

নীচে এর চিত্রে তরঙ্গ দৈর্ঘ্য অনুসারে তড়িৎচুম্বকীয় বর্ণালী দেওয়া হল -

আলোকের বিক্ষেপণ (Scattering of light):
বায়ুমণ্ডলে অবস্থিত বিভিন্ন গ্যাসীয় অনু অপেক্ষাকৃত দীর্ঘ তরঙ্গের আলো শোষণ করে এবং ওই শোষিত আলোক তরঙ্গ চতুর্দিক ছড়িয়ে দেয় । এই ঘটনাকে আলোর বিক্ষেপণ বলে । এক্ষেত্রে ছড়িয়ে দেওয়া আলোর তরঙ্গ দৈর্ঘ্য ও শোষিত আলোর তরঙ্গদৈর্ঘ্য একই হয় । বিক্ষেপিত আলোর তীব্রতা সংশ্লিষ্ট আলোর তরঙ্গদৈর্ঘ্যের চতুর্ঘাতের ব্যস্তানুপাতিক । (I ∝ 1/ λ⁴)

এই কারণে নীল আলোর বিক্ষেপ লাল আলোর তুলনায় বেশী হয় ( নীল আলোর তরঙ্গদৈর্ঘ্য লাল আলোর তুলনায় কম) এই জন্য আকাশকে নীল দেখায় । চাঁদের আকাশ কালো দেখায় কারণ ওখানে বায়ুমণ্ডল না থাকায় আলোর কোনো বিক্ষেপণ হয় না ।
গোলীয় দর্পনে আলোর প্রতিফলন (Reflection at Spherical Mirror):
সমতল দর্পনে সমান্তরাল আলোক রশ্মি গুচ্ছ আপতিত হলে সমান্তরাল আলোক রশ্মি গুচ্ছ হিসাবেই প্রতিফলিতা হয় । কিন্তু গোলীয় দর্পনে সমান্তরাল আলোকরশ্মি গুচ্ছ প্রতিফলিত হলে অভিসারী বা অপসারী আলোকরশ্মি গুচ্ছে পরিণত হয় । যে দর্পন কোনো গোলকের তলের অংশ বিশেষ হয় তাকে গোলীয় দর্পন বলে ।
গোলীয় দর্পন দুই প্রকারের হয় - 1) অবতল দর্পন(Concave Mirror) 2) উত্তল দর্পন (Convex Mirror)
অবতল দর্পন (Concave Mirror) :
যে গোলীয় দর্পনের অবতল পৃষ্ট প্রতিফলক হিসাবে বাবহৃত হয় তাকে অবতল দর্পন বলে ।
উত্তল দর্পন ( Convex Mirror) :
যে গোলীয় দর্পনের উত্তল পৃষ্টে আলোর প্রতিফলন ঘটে তাকে উত্তল দর্পন বলে ।
গোলীয় দর্পনের বক্রতা কেন্দ্র , বক্রতা ব্যাসার্ধ , মেরু ও প্রধান অক্ষ ,ফোকাস দর্ঘ্য :
বক্রতাকেন্দ্র ( Centre of Curvature) :
কোনো গোলীয় দর্পন যে গোলকের অংশ সেই গোলকের কেন্দ্রকে ওই দর্পনের বক্রতা কেন্দ্র বলে ।
বক্রতাব্যাসার্ধ (Radius of Curvature) :
গোলীয় দর্পন যে গোলকের অংশ তার ব্যাসার্ধকেই ওই গোলীয় দর্পনের বক্রতা ব্যাসার্ধ বলে ।
মেরু (Pole) :
কোনো গোলীয় দর্পনের মধ্য বিন্দুকে দার্পনটির মেরু বলে ।
প্রধান অক্ষ ( Principal Axis):
গোলীয় দর্পনের বক্রতা কেন্দ্র ও মেরুর সংযোজক সরলরেখাকে প্রধান অক্ষ বলে ।
ফোকাস দৈঘ্র্য ( Focal Length):
মেরু এবং মুখ্য ফোকাসের মধ্যবর্তী দূরত্বকে ফোকাস দৈর্ঘ্য বলে ।
মুখ্যফোকাস (Principal Focus):
প্রধান অক্ষের সমান্তরাল এক গুচ্ছ সমান্তরাল আলোকরশ্মি অবতল দর্পনে প্রতিফলিত হয়ে প্রধান অক্ষের উপর যে বিন্দুতে মিলিত হয় সেই বিন্দুকে অবতল দর্পনের মুখ্য ফোকাস বলে ।
অনুরূপ ভাবে বলা যায় প্রধান অক্ষের সমান্তরাল আলোকরশ্মি গুচ্ছ উত্তল দর্পনে প্রতিফলিত হয়ে প্রধান অক্ষের যে বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয় সেই বিন্দুটিকে উত্তল দর্পনটির মুখ্য ফোকাস বলে ।
উপাক্ষিয় রশ্মির ধারণা ও ঊপাখিয় রশ্মির ক্ষেত্রে r = 2f প্রদর্শন :
দর্পনের প্রধান অক্ষের নিকটবর্তী আপতিত আলোকরশ্মিকে বলা হয় উপক্ষিয়(Paraxial Rays) রশ্মি । একটি প্রধান অক্ষের সমান্তরাল উপাখিয় রশ্মি AB প্রতিফলনের পর মুখ্য ফোকাস F এর মধ্য দিয়ে যাবে ।B বিন্দুতে দর্পনের উপর অঙ্কিত লম্ব BC বক্রতা কেন্দ্র C বিন্দু দিয়ে যাবে । চিত্র থেকে পাই - আপতন কোন < ABC = i এবং প্রতিফলন কোন <CBF = r .
প্রতিফলনের সুত্রানুযায়ী , ∠ ABC = ∠ CBF এবং ∠ ABC = ∠ BCF = θ (একান্তর কোন )
∴ r = θ অর্থাৎ ΔABC একটি সমবাহু ত্রিভুজ যার BF = CF | উপক্ষিয় রশ্মির ক্ষেত্রে B এবং P খুব নিকটবর্তী হওয়ায় PF = BF অর্থাৎ F হলো CP এর মধ্য বিন্দু ।
∴ PF = f = 1/2 CP = 1/2 r ( BC = CP =r)
ஃ r = 2f
গোলীয় দর্পনে আলোর প্রতিফলনের জন্য প্রতিবিম্ব গঠন :
গোলীয় দর্পনে প্রতিবিম্ব গঠনের নিয়ম : 1 )প্রধান অক্ষের সমান্তরাল আলোক রশ্মি প্রতিফলনের পর মুখ্য ফোকাস দিয়ে যায় । 2) কোনো আপতিত আলোকরশ্মি মুখ্য ফোকাস দিয়ে গিয়ে প্রতিফলনের পর প্রধান অক্ষের সমান্তরাল হয়ে যায় । 3) বক্রতা কেন্দ্রের মধ্য দিয়ে গমনশীল আলোক রশ্মি লম্ব ভাবে দর্পনে আপতিত হয় , ফলে প্রতিফলনের পর একই পথে বিপরীত দিকে ফিরে যায় । উপরের তিনটি নিয়মের যেকোনো দুটির সাহায্যে আমরা প্রতিবিম্ব গঠন করতে পারি ।
অবতল দর্পনে প্রতিবিম্ব গঠনের নিয়ম :
প্রধান অক্ষের সমান্তরাল আলোকরশ্মি AD প্রতিফলিত হয়ে ফোকাস F এর মধ্য দিয়ে গমন করে । A বিন্দু আগত আর একটি আলোক রশ্মি AE বক্রতা কেন্দ্র C দিয়ে গমন করে প্রতিফলিত হয়ে ওই একই পথে বিপরীত দিকে অগ্রসর হয় । এই দুই আলোকরশ্মি প্রতিফলনের পরে A ' বিন্দুতে মিলিত হয় । A' বিন্দুই হল A বিন্দুর সৎবিম্ব ।
অবতল দর্পনে যদি বস্তু ফোকাস দূরত্বের বাইরে থাকে তাহলে বস্তুর একটি সৎবিম্ব গঠিত হয় । আর যদি বস্তু ফোকাস দূরত্বের মধ্যে অবস্থান করে তাহলে বস্তুটির একটি অসৎবিম্ব গঠিত হয় ।
উত্তল দর্পনে প্রতিবিম্ব গঠন :
উত্তল দর্পনে সবসময় খর্বাকৃতি অসৎপ্রতিবিম্ব গঠিত হয় ।
আলোর প্রতিসরণ ( Refraction of Light) :
আলোকরশ্মি যখন এক সমসত্ত্ব সচ্ছ মাধ্যম থেকে অন্য একটি সচ্ছ সমসত্ম মাধ্যমে তীর্যক ভাবে প্রবেশ করে তখন দুই মাধ্যমের বিভেদতলে আলোকরশ্মি অভিমুখ পরিবর্তন করে । এই ঘটনাকে আলোকের প্রতিসরণ বলে ।
প্রতিসরণের সূত্রাবলি ( laws of Refraction):
প্রথম সূত্র : আপতিত রশ্মি , প্রতিসৃত রশ্মি ও আপতন বিন্দুতে দুই মাধ্যমের বিভেদ তলের উপর অঙ্কিত অভিলম্ব একই সমতলে থাকে ।
দ্বিতীয় সূত্র : দুটি নিৰ্দিষ্ট মাধ্যমের বিভেদতলে একটি নিৰ্দিষ্ট বর্ণের আলোর প্রতিসরণ হলে আপতন কোনের সাইন ও প্রতিসরণ কোনের সাইন এর অনুপাত সর্বদা ধ্রুবক থাকে ।
দ্বিতীয় সূত্র অনুসারে পাই ,
sin θi / sin θr = n₁/n₂ = ধ্রুবক = ₁n₂; n₁ হল প্রথম মাধ্যমের পরম প্রতিসরাঙ্ক n₂ হল দ্বিতীয় মাধ্যমের পরম প্রতিসরাঙ্ক ।₁n₂ হল প্রথম মাধ্যমের সাপেক্ষে দ্বিতীয় মাধ্যমের প্রতিসরাঙ্ক ।উপরের সূত্রটিকে স্নেলের সূত্র বলে ।
প্রতিসরাক তলের সঙ্গে লম্বভাবে আলোকরশ্মির আপতনের ক্ষেত্রে স্নেলের সূত্রটি(sin θi / sin θr = n₁/n₂ = ধ্রুবক = ₁n₂ ) প্রযোজ্য নয় ।
প্রতিসরণের সময় আলোকরশ্মি যে কোনে বেঁকে যায় তাকে চ্যুতি বলে ।
লঘু থেকে ঘন মাধ্যমে প্রতিসরণের সময় চ্যুতি :
স্নেলের সূত্র থেকে পাই n2 > n1
অর্থাৎ sin θi / sin θr > 1 ⇒sin θi > sin θr
∴ θi > θr হয় ।
প্রতিসৃত রশ্মিটি অভিলম্বের দিকে সরে যায় । এক্ষেত্রে চ্যুতি হয় (θi - θr) ।
ঘন মাধ্যম থেকে লঘু মাধ্যামে প্রতিসরণের সময় চ্যুতি :
এক্ষেত্রে চ্যুতি d = r - i
প্রিজম (Prism):
তিনটি আয়তাকার তল ও দুটি ত্রিভুজাকার তল দ্বারা সীমাবদ্ধ সচ্ছ প্রতিসারক মাধ্যমকে প্রিজম বলে ।
প্রতিসরাক তল :
যে আয়তাকার তলগুলিতে আলো আপতিত হলে আলোর প্রতিসরণ হয় সেই তলগুলিকে প্রতিসারক তল বলে । প্রিজমে আয়তাকার তলগুলি প্রতিসারক হয় ।
প্রতিসারক কোন :
দুটি প্রতিসারক তল মিলিত হয়ে কোণ উৎপন্ন হয় তাকে পপ্রিজমের প্রতিসারক কোন বলে ।
প্রান্ত রেখা :
প্রিজমের দুটি প্রতিসারক তল যে রেখায় মিলিত হয় তাকে প্রান্ত রেখা বলে ।
ভূমি :
প্রিজমের যে কোনো প্রান্তরেখার বিপরীত তলকে ভূমি বলে ।
প্রধান ছেদ : যে তল প্রিজমের প্রতিসারক তলকে লম্ব ভাবে ছেদ করে তাকে প্রাধান ছেদ বলে ।
প্রিজমের মধ্য দিয়ে প্রতিসৃত রশ্মির চ্যুতি কোন :
ধরা যাক ABC হল প্রিজমের একটি প্রধান ছেদ । A হল প্রিজম কোন ।প্রিজমটির উপাদানের প্রতিসরাঙ্ক μ ।
AB প্রতিসরাক তলে আপতিত রশ্মির আপতন কোন i1 এবং প্রতিসরণ কোন r1 |অনুরূপভাবে AC প্রতিসরাক তলে আপতন কোন r2 এবং প্রতিসরণ কোন ( নির্গমন কোন) i2 | আপতিত ও নির্গমন রশ্মির মধ্যে চ্যুতি কোন∠ LMQ = δ । চিত্র থেকে পাই ∠ MPQ = (i1 - r1 ) এবং ∠MQP = (i2 -r2 ) |
ஃ চ্যুতি কোন δ = ∠ MPQ + ∠MQP = (i1 - r1 ) +(i2 -r2 ) = (i1 + i2 ) -(r1 +r2)
APNQ চতুর্ভূজ থেকে পাওয়া যায়
∠A + ∠N = 180 ডিগ্রী ।( ∠APN = ∠ AQN = 90 ডিগ্রী ।)
আবার PQN ত্রিভুজ থেকে পাই ∠ N + r1 +r2 = 180 ডিগ্রী ।
⇒ r1 +r2 = A
ஃ δ = i₁ +i₂-(r₁ +r₂) = i₁ +i₂ - A
⇒ δ = i₁ +i₂ - A
কাঁচের স্ল্যাবের মধ্য দিয়ে আলোর প্রতিসরণ :
সমান্তরাল পৃষ্ঠযুক্ত একটি কাঁচের ফলকের মধ্য দিয়ে আলোর প্রতিসরণের সময় আলোকরশ্মির কোনো কৌণিক চ্যুতি হয় না ।
উপরের চিত্রে AB আপতিত রশ্মি BC প্রতিসৃত রশ্মি C বিন্দুতে পুনরায় প্রতিসৃত হয়ে CD পথে বহির্গত হয় ।
A বিন্দুতে প্রতিসরণের বেলাই লেখা যায় ,
Sini₁ /Sinr₁= μ ( μ কাঁচের প্রতিসরাঙ্ক ) অনুরূপে C বিন্দুতে প্রতিসরণের ক্ষেত্রে লেখা যায় ,
Sin i₂/ Sinr₂ = 1/μ
এখানে r₁ = i₂ ( B ও C বিন্দুতে অভিলম্ব দুইটি সমান্তরাল ।)
∴ sini₁ /sinr₁ = Sinr₂ / Sini₂
⇒ Sin i₁ = Sinr₂
∴ i₁ = r₂ আপতিত রশ্মি ও নির্গত রশ্মি পরস্পর সমান্তরাল ।
লেন্স (Lens):
দুটি গোলীয় তল বা একটি গোলীয় ও একটি সমতল দ্বারা সীমাবদ্ধ সচ্ছ প্রতিসরাক মাধ্যমকে লেন্স বলে ।
লেন্স প্রধানত দুই প্রকারের হয় । উত্তল লেন্স ও অবতল লেন্স ।
উত্তল লেন্স (Convex lens):
যে লেন্সের মধ্যভাগ মোটা ও প্রান্তের দুই দিক ক্রমশ সরু সেই লেন্সকে উত্তল লেন্স বা অভিসারী লেন্স বলে ।
অবতল লেন্স (Concave lens) :
যে লেন্সের মধ্য ভাগ সরু প্রান্তের দুই ক্রমশ মোটা তাকে অপসারী বা অবতল লেন্স বলে ।
লেন্স সম্পর্কিত কয়কেটি সংজ্ঞা (Some definitions about lens):
বক্রতা কেন্দ্র ( Centre of Curvature) : লেন্সের কোনো গোলীয় তল যে গোলকের অংশ সেই গোলকের কেন্দ্রকে ওই প্রতিসরাক তলের বক্রতা কেন্দ্র বলে ।দুটি গোলীয় তল বিশিষ্ট লেন্সের দুটি বক্রতা কেন্দ্র থাকে ।
বক্রতা ব্যাসার্ধ (Radius of Curvature):
লেন্সের কোনো গোলীয় তল যে গোলকের অংশ সেই গোলকের ব্যাসার্ধকে ওই তলের বক্রতা ব্যাসার্ধ বলে ।
প্রধান অক্ষ (Principal axis):
লেন্সের দুটি বক্রতা কেন্দ্রের সংযোজক সরলরেখাকে লেন্সটির প্রধান অক্ষ বলে ।
উন্মেষ (Aperture): লেন্সের ব্যাসকে উন্মেষ বলে ।
সরু বা পাতলা লেন্স (Thin lens):
লেন্সের প্রধান অক্ষ লেন্সটির দুটি গোলীয় তলকে যে দুটি বিন্দুতে ছেদ করে সেই দুটি বিন্দুর দুরত্ব কে ওই লেন্সের বেধ (Thickness ) বলে । যে লেন্সের বেধ তার বক্রতা ব্যাসার্ধ অপেক্ষা খুব ছোটো সেই লেন্সকে পাতলা লেন্স বলে ।
আলোককেন্দ্র (Optical centre):
আলোককেন্দ্র হল লেন্সের অভ্যন্তরে প্রধানক্ষের উপরে এমন একটি বিন্দু যে বিন্দুর মধ্যে দিয়ে কোনো আলোকরশ্মি গমন করলে ওর কোনো অভিমুখের পরিবর্তন হয় না । অর্থাৎ নির্গত রশ্মি আপতিত রশ্মির সমান্তরাল হয় ।
ফোকাস ,ফোকাস দূরত্ব (Focus, Focul length):
উত্তল লেন্সের ক্ষেত্রে প্রধান অক্ষের সমান্তরাল আলোকরশ্মি গুচ্ছ লেন্সের দ্বারা প্রতিসৃত হয়ে প্রাধান অক্ষের উপর যে বিন্দুতে মিলিত হয় অথবা অবতল লেন্সের ক্ষেত্রে যে বিন্দু থেকে অপসৃত হচ্ছে বলে মনে হয় ,সেই বিন্দুকে লেন্সটির প্রধান বা মুখ্য ফোকাস বলে ।।
লেন্সের আলোককেন্দ্র থেকে প্রধান ফোকাস পর্যন্ত দূরত্বকে ফোকাস দুরত্ব বলে । একে f চিহ্ন দ্বারা প্রকাশ করা হয় ।
উত্তল লেন্সকে অভিসারী লেন্স বলা হয় কারণ প্রধান অক্ষের সমান্তরাল আলোকরশ্মি উত্তল কর্তৃক প্রতিসৃত হয়ে অভিসারী আলোকরশ্মি গুছে পরিণত হয় ।অন্যদিকে অবতল লেন্সকে অপসারী লেন্স বলে কারণ এতে প্রধান অক্ষের সমান্তরাল রশ্মিগুচ্ছ প্রতিসৃত হয়ে অপসারী অলোকরশ্মি গুচ্ছে পরিণত হয় ।
উত্তল লেন্স দ্বারা প্রতিবিম্ব গঠন (Formation of image by convex lens):
উত্তল লেন্সের ক্ষেত্রে প্রতিবিম্ব গঠনের সময় নিম্নলিখিত ধর্মগুলি কাজে লাগানো হয় -
1) প্রধান অক্ষের উপর লম্বভাবে অবস্থিত বস্তুর প্রতিবিম্বও প্রধান অক্ষের উপর লম্ব হয় ।
2) যে রশ্মি গুলি প্রধান অক্ষের প্রধান অক্ষের সমান্তরাল ভাবে আপতিত হয় সেই রশ্মিগুলি প্রতিসরণের পর প্রধান ফোকাস দিয়ে গমন করে ।
3) যে রশ্মিগুলি আলোককেন্দ্র দিয়ে যায় সেগুলির কোনো অভিমুখের পরিবর্তন হয় না ।
রশ্মিচিত্র গঠন (Construction of ray diagram) :
1. বস্তু যখন অসীম দূরত্বে অবস্থিত :
বস্তু অসীম দূরত্বে থাকলে প্রতিবিম্ব ফোকাস তলে গঠিত হয় । প্রতিবিম্ব সৎ, উল্টানো ও আকারে খুব ছোটো হয় ।
2.বস্তু লেন্স থেকে 2f অপেক্ষা বেশি দূরে অবস্থিত :
এক্ষেত্রে প্রতিবিম্ব সৎ ,উল্টানো এবং বস্তুর চেয়ে আকারে ছোট হয় ।
AB বস্তুর প্রতিবিম্ব A¹B¹ |
3. বস্তু লেন্স থেকে 2f দূরত্বে অবস্থিত :
এক্ষেত্রে প্রতিবিম্ব সৎ , উল্টানো এবং বস্তুর সমান আকৃতির হয় ।
4. বস্তু f এবং 2f দূরত্বের মধ্যে অবস্থিত :
এক্ষেত্রে সৎ ,উল্টানো ও বস্তুর চেয়ে বড় আকৃতির প্রতিবিম্ব গঠিত হয় ।
5. বস্তু লেন্সের ফোকাসে অবস্থিত :
এখানে প্রতিবিম্বটি অসীমে তৈরি হয় এবং বিশাল আকৃতির সৎ বিম্ব হয় ।
6. বস্তু লেন্সটির ফোকাসের মধ্যে অবস্থিত :
বস্তুকে আলোককেন্দ্র ও ফোকাসের মধ্যে রাখলে বস্তুটি লেন্সটির যেদিকে আছে সেই দিকেই একটি বিবর্ধিত অসৎ সমশীর্ষ প্রতিবিম্ব গঠিত হয় ।
অবতল লেন্সের দ্বারা প্রতিবিম্ব গঠন :
এক্ষেত্রে বস্তুর সবসময় অসৎ সমশীর্ষ ও খর্বাকৃতি প্রতিবিম্ব গঠিত হয় ।
ৰৈখিক বিবর্ধন (Linear magnification) :
প্রতিবিম্ব ও বস্তুর দৈঘ্যের অনুপাতকে ৰৈখিক বিবর্ধন বলে । প্রমান করা যায় যে ৰৈখিক বিবর্ধন প্রতিবিম্ব এর দূরত্ব ও বস্তু দূরত্বের অনুপাতের সমান ।
বিবর্ধক কাচ (Magnifying glass):
এটি হল কম ফোকাস দৈঘ্যের একটি উত্তল লেন্স ।উত্তল লেন্সের ফোকাসের মধ্যে বস্তু ধরলে বস্তুটির একটি বিবর্ধিত অসৎ প্রিতবিম্ব গঠিত হয় ।
মানুষের চোখের দৃষ্টি সমস্যা :
স্বাবাবিক চোখ 25 সেমি থেকে অসীম দূরত্ব পর্যন্ত দেখতে পায় । একে বলা হয় স্বাবাবিক চোখের দৃষ্টির পাল্লা । ত্রুটি পূর্ণ চোখের দৃষ্টির পাল্লা স্বাভাবিক চোখের তুলনায় কম হয় । মানুষের চোখের সাধারণত দুই প্রকারের ত্রুটি দেখা যায় । ১. দীর্ঘ দৃষ্টি ২. স্বল্প দৃষ্টি
1.দীর্ঘ দৃষ্টি (Hypermetropia):
এই ক্ষেত্রে চোখ দূরের জিনিস স্পষ্ট দেখতে পায় ,কিন্ত কাছের জিনিস স্পষ্টভাবে দেখতে পায় না । এক্ষেত্রে স্পষ্ট দর্শনের ন্যূনতম দুরত্ব 25 সেমি অপেক্ষা বেশি হয় । অক্ষিগোলকের আকার ছোটো হলে বা অক্ষি লেন্সের ফোকাস দৈঘ্য বেড়ে গেলে এই রকম ত্রুটি দেখা যায় । ফলে প্রতিবিম্ব রেটিনা তে তৈরি না হয়ে রেটিনার পেছনে তৈরি হয় । এই ত্রুটি দূর করার জন্য উত্তল লেন্সের চশমা ব্যবহার করা হয় । চশমার পাওয়ার পজিটিভ হয় ।
স্বল্প দৃষ্টি (Myopia):
এক্ষেত্রে চোখ কাছের জিনিস স্পষ্ট দেখতে পায় কিন্তু দূরের জিনিস ভালো দেখতে পায় না । দূরের বস্তু থেকে আগত রশ্মিগুচ্ছ চোখের লেন্স দ্বারা প্রতিসৃত হয়ে রেটিনার সামনের বিন্দুতে মিলিত হয় । চোখের লেন্সের ফোকাস দূরত্ব কমে গেলে এই ধরনের ত্রুটি দেখা যায় । এটি প্রতিকারের জন্য অবতল লেন্সের চশমা ব্যবহার করতে হয় ।
চশমার পাওয়ার নেগেটিভ হয় ।
আলোর বিচ্ছুরণ (Dispersion of Light):
যৌগিক আলো কোনো সচ্ছ মাধ্যম যেমন প্রিজমের মধ্যে গিয়ে বিভিন্ন বর্ণে বিভক্ত হওয়ার ঘটনাকে আলোর বিচ্ছুরণ বলে ।
প্রিজমের সাহায্যে সাদা আলোর বিচ্ছুরণ ( Dispersion of white light by prism) :
সাদা আলো প্রিজমের মধ্যে প্রতিসৃত হয়ে সাতটি বিভিন্ন বর্ণের আলোকে বিশ্লিষ্ট হয়ে যায় । এই সাতটি বিভিন্ন বর্ণের যে আলোর পটি পাওয়া যায় তাকে বর্ণালী বলে ।
একটি সাদা আলোকরশ্মি প্রিজমটির প্রথম প্রতিসারক তলে আপতিত হলে ওই রশ্মি থেকে সাতটি আলাদা আলাদা বর্ণের আলোক রশ্মি পাওয়া যায় । বিভিন্ন বর্ণের আলোর প্রতিসরাঙ্ক তথা গতিবেগ বিভিন্ন হওয়ায় বর্ণগুলি পাওয়া যায় । বিভিন্ন বর্ণগুলির চ্যুতিও বিভিন্ন হয় । দ্বিতীয় প্রতিসরাক তল থেকে আরো অধিক বিচ্যুতি নিয়ে বাইরে বেরিয়ে আসে । এখানে দুই প্রতিসরাক তলে বিভিন্ন বর্ণগুলির বিচ্যুতি একই অভিমুখে হয় ফলে বর্ণালী পাওয়া যায় । বিভিন্ন যৌগিক বর্ণগুলি হল বেগুনী ,নীল ,আকাশীনীল ,সবুজ ,হলুদ ,কমলা ও লাল । মনে রাখার জন্য সমস্ত বর্ণগুলির আদ্যাক্ষর নিয়ে একটি শব্দ গঠন করা যায় । শব্দটি হল -বেনীআসহকলা । ইংরেজিতে শব্দটি - VIBGYOR ।
আয়তাকার কাচের স্ল্যাবের মধ্যেদিয়ে সাদা আলো প্রতিসৃত হলে বর্ণালী পাওয়া যায় না কারণ এখানে দুই বিপরীত প্রতিসারক তলে বিভিন্ন বর্ণের আলোগুলির বিচ্যুতি পরস্পর বিপরীত দিকে ঘটে । ফলে মোট বিচ্যুতি শূন্য হয় ।
একবর্ণী আলো (Monochromatic light):
সাদা আলো হল এক প্রকারের যৌগিক আলো ,কারণ সাদা আলো সাতটি বিভিন্ন বর্ণের আলোর সমষ্টি । এই এক একটি বর্ণ হল একবর্ণী আলো । কোনো অসচ্ছ বস্তুর বর্ণ নির্ভর করে বস্তুটি কোন বর্ণের আলো প্রতিফলন করতে পারে তার ওপর । লাল রঙের বস্তুর উপর সাদা আলো পড়লে কেবল লাল রংটি প্রতিফলিত হয় অন্য বর্ণের আলোগুলি শোষিত হয় ।তাই বস্তুটির রঙ লাল হয় । লাল বর্ণের জবা ফুলের উপর নীল আলো পড়লে ফুলটিকে কালো দেখাবে ।
কারণ লাল ফুল নীল রঙ কে শোষণ করে নিবে । জবা ফুল থেকে কোনো বর্ণের আলো প্রতিফলিত হবে না । সুতরাং ফুলটিকে কালো দেখাবে কারণ কালো রঙ হলো সমস্ত রঙের অনুপস্থিতি ।কোনো সচ্ছ বস্তুর বর্ণ নির্ভর করে বস্তুর মধ্য দিয়ে নির্গত আলোর বর্ণের ওপর । নীলবর্ণের কাচের উপর সাদা আলো পড়লে শুধু নীলবর্ণটি কাচের ভিতর দিয়ে নির্গত হবে । অন্য্ বর্ণগুলি শোষিত হবে । ফলে কাচটি নীল দেখাবে ।
আলোকতরঙ্গ ( Light wave) :
আলো এক প্রকারের তড়িৎচুম্বকীয় তির্যক তরঙ্গ ( electromagnetic wave) | এই তরঙ্গ বিস্তারের জন্য কোনো জড় মাধ্যমের প্রয়োজন হয় না ।
তরঙ্গ সম্পর্কিত কয়টি সংজ্ঞা :
কম্পাঙ্ক (Frequency) :
এক সেকেন্ডে কোনো মাধ্যমের মধ্যে যতগুলি পূর্ণ তরঙ্গের সৃষ্টি হয় তাকে তরঙ্গের কম্পাঙ্ক বলে । কম্পাঙ্কের SI একক হলো হার্ৎজ (Hz) |
তরঙ্গদৈর্ঘ্য (Wave length) :
কোনো তরঙ্গের উপরিস্থিত সমদশা সম্পন্ন পরপর দুটি বিন্দুর দূরত্ত্বকে ওই তরঙ্গের তরঙ্গ দৈর্ঘ্য বলে । তরঙ্গদৈর্ঘ্য এর SI একক মিটার ।
তরঙ্গবেগ (Wave velocity):
একক সময়ে কোনো তরঙ্গ যে দূরত্ব অতিক্রম করে তাকে তরঙ্গবেগ বলে । এর SI একক m/s | শূন্য মাধ্যমে সব বর্ণের আলো একই বেগে গমন করে । এই বেগের মান 3 x 10⁸ m/s | কিন্তূ কোনো মাধ্যমে আলোর বেগ উহার তরঙ্গদৈর্ঘ্যের ওপর নির্ভর করে । আলোর তরঙ্গ তত্ত্ব অনুসারে কোনো মাধ্যমের প্রতিসরাঙ্ক শুন্যমাধ্যমে আলোর বেগ ও ওই মাধ্যমে আলোর বেগের অনুপাতের সমান ( μ = c/v ) | বিভিন্ন বর্ণের প্রতিসরাঙ্ক বিভিন্ন হওয়ায় বিভিন্ন বর্ণের আলোর গতিবেগও বিভিন্ন হয় ।লাল বর্ণের গতিবেগ সবচেয়ে বেশি হয় এবং বেগুনি বর্ণের গতিবেগ সবচেয়ে কম হয় ।
নীচে এর চিত্রে তরঙ্গ দৈর্ঘ্য অনুসারে তড়িৎচুম্বকীয় বর্ণালী দেওয়া হল -

আলোকের বিক্ষেপণ (Scattering of light):
বায়ুমণ্ডলে অবস্থিত বিভিন্ন গ্যাসীয় অনু অপেক্ষাকৃত দীর্ঘ তরঙ্গের আলো শোষণ করে এবং ওই শোষিত আলোক তরঙ্গ চতুর্দিক ছড়িয়ে দেয় । এই ঘটনাকে আলোর বিক্ষেপণ বলে । এক্ষেত্রে ছড়িয়ে দেওয়া আলোর তরঙ্গ দৈর্ঘ্য ও শোষিত আলোর তরঙ্গদৈর্ঘ্য একই হয় । বিক্ষেপিত আলোর তীব্রতা সংশ্লিষ্ট আলোর তরঙ্গদৈর্ঘ্যের চতুর্ঘাতের ব্যস্তানুপাতিক । (I ∝ 1/ λ⁴)
এই কারণে নীল আলোর বিক্ষেপ লাল আলোর তুলনায় বেশী হয় ( নীল আলোর তরঙ্গদৈর্ঘ্য লাল আলোর তুলনায় কম) এই জন্য আকাশকে নীল দেখায় । চাঁদের আকাশ কালো দেখায় কারণ ওখানে বায়ুমণ্ডল না থাকায় আলোর কোনো বিক্ষেপণ হয় না ।
নীচের MCQ গুলি উত্তর দাও ( প্রদত্ত লিংক টিতে click বা click না হলে copy করে গুগল ব্রাউজার এ paste কর ):
https://forms.gle/bHQWKdRsny19cbi66



কোন মন্তব্য নেই:
একটি মন্তব্য পোস্ট করুন